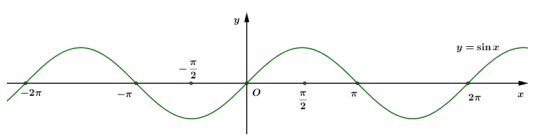
Câu hỏi: Cho đồ thị hàm số y = \sin x như hình dưới, tìm tất cả các số thực $x\in \left[ -\dfrac{\pi }{2};2\pi \right]$ để $\sin \left| x \right|>0$
A. $\left( 0;\pi \right)$
B. $\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$
C. $\left[ -\dfrac{\pi }{2};0 \right)\cup \left( 0;\pi \right)$
D. $\left( -\dfrac{\pi }{2};0 \right)\cup \left( 0;\pi \right)$

A. $\left( 0;\pi \right)$
B. $\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$
C. $\left[ -\dfrac{\pi }{2};0 \right)\cup \left( 0;\pi \right)$
D. $\left( -\dfrac{\pi }{2};0 \right)\cup \left( 0;\pi \right)$
Phương pháp:
Từ đồ thị hàm số đã cho, suy ra đồ thị hàm số $y=\sin \left| x \right|$ bằng cách giữ lại phần đồ thị phía bên phải trục tung và lấy đối xứng phần đồ thị đó qua trục tung.
Cách giải:

Dựa vào đồ thị hàm số $y=\sin \left| x \right|$ ta thấy $\sin \left| x \right|~\Leftrightarrow \left[ \begin{aligned}
& -\dfrac{\pi }{2}<x<0 \\
& 0<x<\pi \\
\end{aligned} \right.$
Từ đồ thị hàm số đã cho, suy ra đồ thị hàm số $y=\sin \left| x \right|$ bằng cách giữ lại phần đồ thị phía bên phải trục tung và lấy đối xứng phần đồ thị đó qua trục tung.
Cách giải:
Dựa vào đồ thị hàm số $y=\sin \left| x \right|$ ta thấy $\sin \left| x \right|~\Leftrightarrow \left[ \begin{aligned}
& -\dfrac{\pi }{2}<x<0 \\
& 0<x<\pi \\
\end{aligned} \right.$
Đáp án D.