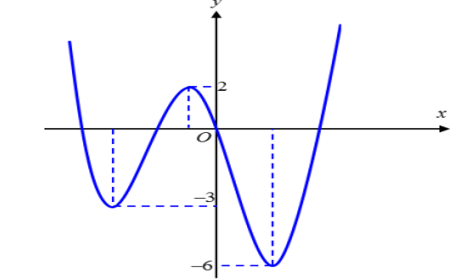
Cho đồ thị hàm số $y=f(x)$ như hình vẽ dưới đây: Gọi $S$ là tập...

Đặt $h\left( x \right)=f(x+2023)+\dfrac{1}{3}{{m}^{2}}\Rightarrow {h}'\left( x \right)={f}'(x+2023).$
Ta có $y=\left| A \right|=\sqrt{{{A}^{2}}}\Rightarrow y'=\dfrac{A.A'}{\sqrt{{{A}^{2}}}}.$
Số cực trị của $y=\left|f(x+2023)+\dfrac{1}{3} m^2\right|$ là số nghiệm đơn hoặc bội lẻ của $h\left( x \right){h}'\left( x \right)=0.$
${h}'\left( x \right)=0\Leftrightarrow {f}'\left( x+2023 \right)=0$ có 3 nghiệm đơn phân biệt.
$m$ để hàm số $y=\left|f(x+2023)+\dfrac{1}{3} m^2\right|$ có 5 điểm cực trị thì $h\left( x \right)=0\Leftrightarrow f(x+2023)=-\dfrac{1}{3}{{m}^{2}}$
Có 2 nghiệm phân biệt. Dựa vào đồ thị điều kiện $\left[ \begin{aligned}
& -6<-\dfrac{1}{3}{{m}^{2}}<-3 \\
& -\dfrac{1}{3}{{m}^{2}}\ge 2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 9\le {{m}^{2}}<18 \\
& {{m}^{2}}\le -6 \\
\end{aligned} \right..$
Do $m$ nguyên dương nên $m=4,m=3.$
Tổng các giá trị các phần tử của tập $S$ là $3+4=7.$