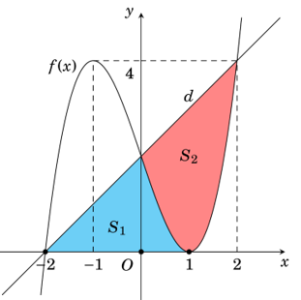
Câu hỏi: Cho đồ thị hàm số bậc ba $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ và đường thẳng $d:y=mx+n$ như hình vẽ và ${{S}_{1}},{{S}_{2}}$ là diện tích hình phẳng được tô đậm trong hình bên. Biết $\dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{p}{q}$ với $p,q\in {{\mathbb{N}}^{*}}$ là một phân số tối giản. Tính $p+q+2022$.
A. $2043$.
B. $2045$.
C. $2049$.
D. $2051$.
A. $2043$.
B. $2045$.
C. $2049$.
D. $2051$.
Ta có ${y}'={f}'\left( x \right)=3a{{x}^{2}}+2bx+c$.
Do đồ thị hàm số $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có hai điểm cực trị là $\left( -1\text{ ; 4} \right)$ và $\left( 1\text{ ; 0} \right)$ nên
$\left\{ \begin{aligned}
& 3a-2b+c=0 \\
& 3a+2b+c=0 \\
& -a+b-c+d=4 \\
& a+b+c+d=0 \\
\end{aligned} \right.\Rightarrow \left\{ \begin{aligned}
& a=1 \\
& b=0 \\
& c=-3 \\
& d=2 \\
\end{aligned} \right.$$\Rightarrow y={{x}^{2}}-3x+2$.
Vì đường thẳng $d:y=mx+n$ đi qua 2 điểm $\left( -2\text{ ; 0} \right),\left( \text{0 ; 2} \right)$ nên $d:y=x+2$.
Ta có ${{S}_{1}}=\dfrac{1}{2}{{.2}^{2}}+\int\limits_{0}^{1}{\left| {{x}^{3}}-3x+2 \right|\text{d}x=}2+\int\limits_{0}^{1}{\left( {{x}^{3}}-3x+2 \right)\text{d}x=}$ $=2+\left. \left( \dfrac{{{x}^{4}}}{4}-\dfrac{3{{x}^{2}}}{2}+2x \right) \right|_{0}^{1}=\dfrac{11}{4}$.
${{S}_{2}}=\int\limits_{0}^{2}{\left| \left( x+2 \right)-\left( {{x}^{3}}-3x+2 \right) \right|\text{d}x=}\int\limits_{0}^{2}{\left( x+2-{{x}^{3}}+3x-2 \right)\text{d}x=}\int\limits_{0}^{2}{\left( -{{x}^{3}}+4x \right)\text{d}x=}4$.
$\Rightarrow \dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{p}{q}=\dfrac{11}{16}$.
Vậy $p+q+2022=2049$.
Do đồ thị hàm số $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có hai điểm cực trị là $\left( -1\text{ ; 4} \right)$ và $\left( 1\text{ ; 0} \right)$ nên
$\left\{ \begin{aligned}
& 3a-2b+c=0 \\
& 3a+2b+c=0 \\
& -a+b-c+d=4 \\
& a+b+c+d=0 \\
\end{aligned} \right.\Rightarrow \left\{ \begin{aligned}
& a=1 \\
& b=0 \\
& c=-3 \\
& d=2 \\
\end{aligned} \right.$$\Rightarrow y={{x}^{2}}-3x+2$.
Vì đường thẳng $d:y=mx+n$ đi qua 2 điểm $\left( -2\text{ ; 0} \right),\left( \text{0 ; 2} \right)$ nên $d:y=x+2$.
Ta có ${{S}_{1}}=\dfrac{1}{2}{{.2}^{2}}+\int\limits_{0}^{1}{\left| {{x}^{3}}-3x+2 \right|\text{d}x=}2+\int\limits_{0}^{1}{\left( {{x}^{3}}-3x+2 \right)\text{d}x=}$ $=2+\left. \left( \dfrac{{{x}^{4}}}{4}-\dfrac{3{{x}^{2}}}{2}+2x \right) \right|_{0}^{1}=\dfrac{11}{4}$.
${{S}_{2}}=\int\limits_{0}^{2}{\left| \left( x+2 \right)-\left( {{x}^{3}}-3x+2 \right) \right|\text{d}x=}\int\limits_{0}^{2}{\left( x+2-{{x}^{3}}+3x-2 \right)\text{d}x=}\int\limits_{0}^{2}{\left( -{{x}^{3}}+4x \right)\text{d}x=}4$.
$\Rightarrow \dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{p}{q}=\dfrac{11}{16}$.
Vậy $p+q+2022=2049$.
Đáp án C.