Google
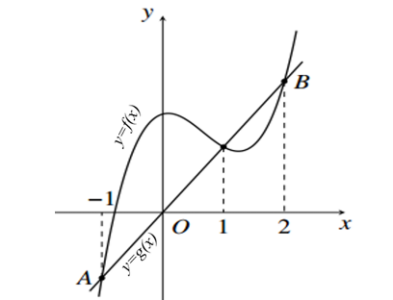
Câu hỏi: Cho đồ thị hàm số bậc ba $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+\dfrac{1}{3}x+c$ và đường thẳng $y=g\left( x \right)$ có đồ thị như hình vẽ sau:
Biết $AB=5$, diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=1$, $x=2$ bằng
A. $\dfrac{17}{11}$.
B. $\dfrac{19}{12}$.
C. $\dfrac{5}{12}$.
D. $\dfrac{7}{11}$.
Khi đó $AB=\sqrt{9+9{{m}^{2}}}=5\Leftrightarrow \left[ \begin{aligned}
& m=\dfrac{4}{3}\left( tm \right) \\
& m=-\dfrac{4}{3}\left( l \right) \\
\end{aligned} \right.$.
Ta có $f\left( x \right)=g\left( x \right)\Leftrightarrow a{{x}^{3}}+b{{x}^{2}}-x+c=0$.
Mặt khác $a{{x}^{3}}+b{{x}^{2}}-x+c=a\left( {{x}^{2}}-1 \right)\left( x-2 \right)$ $\Leftrightarrow a{{x}^{3}}+b{{x}^{2}}-x+c=a{{x}^{3}}-2a{{x}^{2}}-ax+2a$,
Đồng nhất hệ số ta đươc $a=1$, $b=-2$, $c=2$. Vậy $y=f\left( x \right)={{x}^{3}}-2{{x}^{2}}+\dfrac{1}{3}x+2$.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=1$, $x=2$ bằng $S=\int\limits_{1}^{2}{\left( {{x}^{3}}-2{{x}^{2}}+\dfrac{1}{3}x+2 \right)\text{d}x}=\dfrac{19}{12}.$
A. $\dfrac{17}{11}$.
B. $\dfrac{19}{12}$.
C. $\dfrac{5}{12}$.
D. $\dfrac{7}{11}$.
Gọi $g\left( x \right)=mx\left( m>0 \right)$. Ta có $A\left( -1 ; -m \right) $ ; $B\left( 2 ; 2m \right)$.Khi đó $AB=\sqrt{9+9{{m}^{2}}}=5\Leftrightarrow \left[ \begin{aligned}
& m=\dfrac{4}{3}\left( tm \right) \\
& m=-\dfrac{4}{3}\left( l \right) \\
\end{aligned} \right.$.
Ta có $f\left( x \right)=g\left( x \right)\Leftrightarrow a{{x}^{3}}+b{{x}^{2}}-x+c=0$.
Mặt khác $a{{x}^{3}}+b{{x}^{2}}-x+c=a\left( {{x}^{2}}-1 \right)\left( x-2 \right)$ $\Leftrightarrow a{{x}^{3}}+b{{x}^{2}}-x+c=a{{x}^{3}}-2a{{x}^{2}}-ax+2a$,
Đồng nhất hệ số ta đươc $a=1$, $b=-2$, $c=2$. Vậy $y=f\left( x \right)={{x}^{3}}-2{{x}^{2}}+\dfrac{1}{3}x+2$.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=1$, $x=2$ bằng $S=\int\limits_{1}^{2}{\left( {{x}^{3}}-2{{x}^{2}}+\dfrac{1}{3}x+2 \right)\text{d}x}=\dfrac{19}{12}.$
Đáp án B.