Câu hỏi: a) Tính \(x = \cos \dfrac{{2\pi }}{5}\) bằng “phương pháp hình học” như sau:
Xét tam giác cân ABC với \(\widehat B = \widehat C = \dfrac{{2\pi }}{5}\), kẻ đường phân giác BD của tam giác đó. Từ tính chất \(\dfrac{{BC}}{{BA}} = \dfrac{{DC}}{{DA}}\) (h. 6.7) hãy suy ra \(4{x^2} + 2x - 1 = 0\).
b) Từ đó tính \(\cos \dfrac{\pi }{5},\sin \dfrac{\pi }{5},\tan \dfrac{\pi }{5}\).
c) Tính sin, côsin, tang của \({18^0}\)
d) Viết \(6 = 36 - 30\), tính sin, côsin của \({6^0}\). Thử lại bằng má tính bỏ túi.
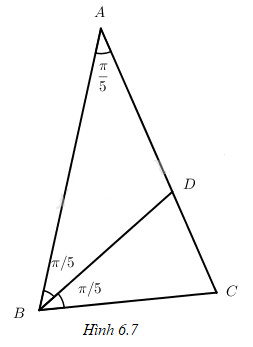
Xét tam giác cân ABC với \(\widehat B = \widehat C = \dfrac{{2\pi }}{5}\), kẻ đường phân giác BD của tam giác đó. Từ tính chất \(\dfrac{{BC}}{{BA}} = \dfrac{{DC}}{{DA}}\) (h. 6.7) hãy suy ra \(4{x^2} + 2x - 1 = 0\).
b) Từ đó tính \(\cos \dfrac{\pi }{5},\sin \dfrac{\pi }{5},\tan \dfrac{\pi }{5}\).
c) Tính sin, côsin, tang của \({18^0}\)
d) Viết \(6 = 36 - 30\), tính sin, côsin của \({6^0}\). Thử lại bằng má tính bỏ túi.

Lời giải chi tiết
a) Dễ thấy \(BC = BD = AD\), nên đặt \(BC = a, AB = b\) thì \(\cos \dfrac{{2\pi }}{5} = \dfrac{a}{{2b}}.\) (1)
Ta có \(\dfrac{{DC}}{{DA}} = \dfrac{{BC}}{{BA}}\) suy ra \(\dfrac{{b - a}}{a} = \dfrac{a}{b}\), tức là \(\dfrac{{1 - \dfrac{a}{b}}}{{\dfrac{a}{b}}} = \dfrac{a}{b}.\) (2)
Từ (1) và (2) ta có \(\dfrac{{1 - 2\cos \dfrac{{2\pi }}{5}}}{{2\cos \dfrac{{2\pi }}{5}}} = 2\cos \dfrac{{2\pi }}{5}\) hay
\(4{\cos ^2}\dfrac{{2\pi }}{5} + 2\cos \dfrac{{2\pi }}{5} - 1 = 0\), tức là \(4{x^2} + 2x - 1 = 0\). (3)
b) Giải phương trình (3), ta được \(x = \dfrac{{ - 1 - \sqrt 5 }}{4}\) hoặc \(x = \dfrac{{ - 1 + \sqrt 5 }}{4}\) .
Từ đó \(\cos \dfrac{{2\pi }}{5} = \dfrac{{ - 1 - \sqrt 5 }}{4} < 0\) (loại) hoặc \(\cos \dfrac{{2\pi }}{5} = \dfrac{{\sqrt 5 - 1}}{4}.\) Suy ra
\(\begin{array}{l}\cos \dfrac{\pi }{5} = \sqrt {\dfrac{{1 + \cos \dfrac{{2\pi }}{5}}}{2}} = \sqrt {\dfrac{{3 + \sqrt 5 }}{8}} = \dfrac{{\sqrt 5 + 1}}{4};\\sin\dfrac{\pi }{5} = \sqrt {\dfrac{{1 - \cos \dfrac{{2\pi }}{5}}}{2}} = \sqrt {\dfrac{{10 - 2\sqrt 5 }}{4}} ;\\\tan \dfrac{\pi }{5} = \dfrac{{\sin \dfrac{\pi }{5}}}{{\cos \dfrac{\pi }{5}}} = \sqrt {5 - r\sqrt 5 .} \end{array}\)
c)
\(\begin{array}{l}\sin {18^0} = \sin \dfrac{\pi }{{10}} = \sin \left( {\dfrac{1}{2}.\dfrac{\pi }{5}} \right)\\ = \sqrt {\dfrac{{1 - \cos \dfrac{\pi }{5}}}{2}} = \dfrac{1}{4}\sqrt {2\left({3 - \sqrt 5 } \right)} .\end{array}\)
\(\begin{array}{l}\cos {18^0} = \cos \dfrac{\pi }{{10}} = \cos \left( {\dfrac{1}{2}.\dfrac{\pi }{5}} \right)\\ = \sqrt {\dfrac{{1 + \cos \dfrac{\pi }{5}}}{2}} = \dfrac{1}{4}\sqrt {2\left({5 + \sqrt 5 } \right)} .\end{array}\)
\(\tan {18^0} = \dfrac{{\sin {{18}^0}}}{{\cos {{18}^0}}} = \sqrt {1 - \dfrac{{2\sqrt 5 }}{5}} .\)
d)
\(\begin{array}{l}\sin {6^0} = \sin \left( {{{36}^0} - {{30}^0}} \right) = \sin \left({\dfrac{\pi }{5} - \dfrac{\pi }{6}} \right)\\ = \sin \dfrac{\pi }{5}\cos \dfrac{\pi }{6} - \cos \dfrac{\pi }{5}\sin \dfrac{\pi }{6}\\ = \dfrac{{\sqrt 3 }}{2}\sin \dfrac{\pi }{5} - \dfrac{1}{2}\cos \dfrac{\pi }{5}\\ = \dfrac{1}{8}\left[ {\sqrt {6\left({5 - \sqrt 5 } \right)} - \left({\sqrt 5 + 1} \right)} \right]\left({ \approx 0,1045} \right).\end{array}\)
\(\begin{array}{l}\cos {6^0} = \cos \left( {{{36}^0} - {{30}^0}} \right) = \cos \left({\dfrac{\pi }{5} - \dfrac{\pi }{6}} \right)\\ = \cos \dfrac{\pi }{5}\cos \dfrac{\pi }{6} + \sin \dfrac{\pi }{5}\sin \dfrac{\pi }{6}\\ = \dfrac{{\sqrt 3 }}{2}\cos \dfrac{\pi }{5} + \dfrac{1}{2}\sin \dfrac{\pi }{5}\\ = \dfrac{1}{8}\left[ {\sqrt 3 \left({\sqrt 5 + 1} \right) + \sqrt {2\left({5 - \sqrt 5 } \right)} } \right]\left({ \approx 0,9945} \right).\end{array}\)
a) Dễ thấy \(BC = BD = AD\), nên đặt \(BC = a, AB = b\) thì \(\cos \dfrac{{2\pi }}{5} = \dfrac{a}{{2b}}.\) (1)
Ta có \(\dfrac{{DC}}{{DA}} = \dfrac{{BC}}{{BA}}\) suy ra \(\dfrac{{b - a}}{a} = \dfrac{a}{b}\), tức là \(\dfrac{{1 - \dfrac{a}{b}}}{{\dfrac{a}{b}}} = \dfrac{a}{b}.\) (2)
Từ (1) và (2) ta có \(\dfrac{{1 - 2\cos \dfrac{{2\pi }}{5}}}{{2\cos \dfrac{{2\pi }}{5}}} = 2\cos \dfrac{{2\pi }}{5}\) hay
\(4{\cos ^2}\dfrac{{2\pi }}{5} + 2\cos \dfrac{{2\pi }}{5} - 1 = 0\), tức là \(4{x^2} + 2x - 1 = 0\). (3)
b) Giải phương trình (3), ta được \(x = \dfrac{{ - 1 - \sqrt 5 }}{4}\) hoặc \(x = \dfrac{{ - 1 + \sqrt 5 }}{4}\) .
Từ đó \(\cos \dfrac{{2\pi }}{5} = \dfrac{{ - 1 - \sqrt 5 }}{4} < 0\) (loại) hoặc \(\cos \dfrac{{2\pi }}{5} = \dfrac{{\sqrt 5 - 1}}{4}.\) Suy ra
\(\begin{array}{l}\cos \dfrac{\pi }{5} = \sqrt {\dfrac{{1 + \cos \dfrac{{2\pi }}{5}}}{2}} = \sqrt {\dfrac{{3 + \sqrt 5 }}{8}} = \dfrac{{\sqrt 5 + 1}}{4};\\sin\dfrac{\pi }{5} = \sqrt {\dfrac{{1 - \cos \dfrac{{2\pi }}{5}}}{2}} = \sqrt {\dfrac{{10 - 2\sqrt 5 }}{4}} ;\\\tan \dfrac{\pi }{5} = \dfrac{{\sin \dfrac{\pi }{5}}}{{\cos \dfrac{\pi }{5}}} = \sqrt {5 - r\sqrt 5 .} \end{array}\)
c)
\(\begin{array}{l}\sin {18^0} = \sin \dfrac{\pi }{{10}} = \sin \left( {\dfrac{1}{2}.\dfrac{\pi }{5}} \right)\\ = \sqrt {\dfrac{{1 - \cos \dfrac{\pi }{5}}}{2}} = \dfrac{1}{4}\sqrt {2\left({3 - \sqrt 5 } \right)} .\end{array}\)
\(\begin{array}{l}\cos {18^0} = \cos \dfrac{\pi }{{10}} = \cos \left( {\dfrac{1}{2}.\dfrac{\pi }{5}} \right)\\ = \sqrt {\dfrac{{1 + \cos \dfrac{\pi }{5}}}{2}} = \dfrac{1}{4}\sqrt {2\left({5 + \sqrt 5 } \right)} .\end{array}\)
\(\tan {18^0} = \dfrac{{\sin {{18}^0}}}{{\cos {{18}^0}}} = \sqrt {1 - \dfrac{{2\sqrt 5 }}{5}} .\)
d)
\(\begin{array}{l}\sin {6^0} = \sin \left( {{{36}^0} - {{30}^0}} \right) = \sin \left({\dfrac{\pi }{5} - \dfrac{\pi }{6}} \right)\\ = \sin \dfrac{\pi }{5}\cos \dfrac{\pi }{6} - \cos \dfrac{\pi }{5}\sin \dfrac{\pi }{6}\\ = \dfrac{{\sqrt 3 }}{2}\sin \dfrac{\pi }{5} - \dfrac{1}{2}\cos \dfrac{\pi }{5}\\ = \dfrac{1}{8}\left[ {\sqrt {6\left({5 - \sqrt 5 } \right)} - \left({\sqrt 5 + 1} \right)} \right]\left({ \approx 0,1045} \right).\end{array}\)
\(\begin{array}{l}\cos {6^0} = \cos \left( {{{36}^0} - {{30}^0}} \right) = \cos \left({\dfrac{\pi }{5} - \dfrac{\pi }{6}} \right)\\ = \cos \dfrac{\pi }{5}\cos \dfrac{\pi }{6} + \sin \dfrac{\pi }{5}\sin \dfrac{\pi }{6}\\ = \dfrac{{\sqrt 3 }}{2}\cos \dfrac{\pi }{5} + \dfrac{1}{2}\sin \dfrac{\pi }{5}\\ = \dfrac{1}{8}\left[ {\sqrt 3 \left({\sqrt 5 + 1} \right) + \sqrt {2\left({5 - \sqrt 5 } \right)} } \right]\left({ \approx 0,9945} \right).\end{array}\)