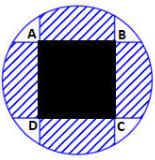
Câu hỏi: Bồn hoa của một trường X có dạng hình tròn bán kính bằng $8 m$. Người ta chia bồn hoa thành các phần như hình vẽ dưới đây và có ý định trồng hoa như sau: Phần diện tích bên trong hình vuông $ABCD$ để trồng hoa. Phần diện tích kéo dài từ 4 cạnh của hình vuông đến đường tròn dùng để trồng cỏ. Ở bốn góc còn lại, mỗi góc trồng một cây cọ. Biết $AB=4m$, giá trồng hoa là $200.000$ đ/ ${{m}^{2}}$, giá trồng cỏ là $100.000$ đ/ ${{m}^{2}}$, mỗi cây cọ giá $150.000$ đ. Hỏi cần bao nhiêu tiền để thực hiện việc trang trí bồn hoa đó.
A. $14.865.000$ đồng.
B. $12.218.000$ đồng.
C. $14.465.000$ đồng.
D. $13.265.000$ đồng.

A. $14.865.000$ đồng.
B. $12.218.000$ đồng.
C. $14.465.000$ đồng.
D. $13.265.000$ đồng.
Gắn hệ trục như hình vẽ (gốc tọa độ là tâm của hình tròn), kí hiệu các điểm như hình vẽ.

Đường tròn có phương trình: ${{x}^{2}}+{{y}^{2}}=64$. Suy ra $y=\pm \sqrt{64-{{x}^{2}}}$.
Phương trình $AB:y=2$.
Diện tích phần trồng cỏ: ${{S}_{1}}=4\int\limits_{-2}^{2}{\left( \sqrt{64-{{x}^{2}}}-2 \right)\text{d}x} \left( {{m}^{2}} \right)$.
Diện tích phần trồng hoa: ${{S}_{2}}=4.4=16 ({{m}^{2}})$.
Số tiền phải bỏ ra là:
$200 000.16+4.150 000+100 000.4\int\limits_{-2}^{2}{\left( \sqrt{64-{{x}^{2}}}-2 \right)\text{d}x}\approx 13 265 000 $ (đồng).
Đường tròn có phương trình: ${{x}^{2}}+{{y}^{2}}=64$. Suy ra $y=\pm \sqrt{64-{{x}^{2}}}$.
Phương trình $AB:y=2$.
Diện tích phần trồng cỏ: ${{S}_{1}}=4\int\limits_{-2}^{2}{\left( \sqrt{64-{{x}^{2}}}-2 \right)\text{d}x} \left( {{m}^{2}} \right)$.
Diện tích phần trồng hoa: ${{S}_{2}}=4.4=16 ({{m}^{2}})$.
Số tiền phải bỏ ra là:
$200 000.16+4.150 000+100 000.4\int\limits_{-2}^{2}{\left( \sqrt{64-{{x}^{2}}}-2 \right)\text{d}x}\approx 13 265 000 $ (đồng).
Đáp án D.