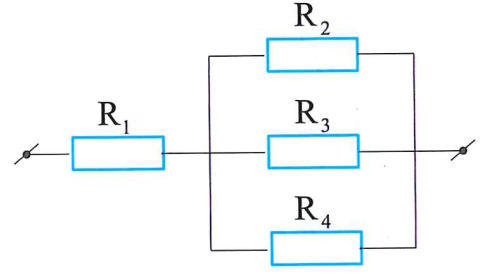
Bốn điện trở ${{R}_{1}}=2\Omega ;{{R}_{2}}=6\Omega...

The Knowledge · 1/1/22

Câu hỏi:

Bốn điện trở

R_{1} = 2 Ω; R_{2} = 6 Ω; R_{3}; R_{4} = 4 Ω

mắc như hình vẽ, hiệu điện thế giữa hai đầu đoạn mạch là 48 V.
Cường độ dòng điện chạy qua

R_{3}

là 2A. Hãy tính điện trở

R_{3}

A.

R_{3} = 15 Ω .

B.

R_{3} = 15, 2 Ω .

C.

R_{3} = 13, 5 Ω .

D.

R_{3} = 12 Ω .

Sơ đồ mạch điện

R_{1} n t (R_{2} / / R_{3} / / R_{4}) .

Đặt

R_{3} = x (Ω) \Rightarrow U_{3} = I_{3} R_{3} = 2 x (V) = U_{2} = U_{4} = U_{234} \Rightarrow U_{1} = U - U_{234} = 48 - 2 x (V)

\Rightarrow I_{2} = \frac{U_{2}}{R_{2}} = \frac{2 x}{6} = \frac{x}{3} (A); I_{4} = \frac{U_{4}}{R_{4}} = \frac{2 x}{4} = \frac{x}{2} (A); I_{1} = \frac{U_{1}}{R_{1}} = \frac{48 - 2 x}{2} = 24 - x (A)

Ta có:

I_{1} = I_{234} = I_{2} + I_{3} + I_{4} \Rightarrow 24 - x = \frac{x}{3} + 2 + \frac{x}{2} \Rightarrow x = 12

.
Vậy

R_{3} = 12 (Ω)

.

Đáp án D.