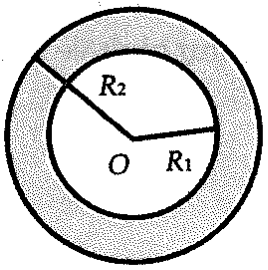
Câu hỏi: Biết săm lốp xe ô tô bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ ${{R}_{1}}=20cm,$ bán kính đường tròn lớn ${{R}_{2}}=30cm,$ và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc với mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày của vỏ săm. Tính thể tích không khí chứa được bên trong săm.
A. $600{{\pi }^{2}}c{{m}^{3}}.$
B. $1400\pi c{{m}^{3}}.$
C. $1250{{\pi }^{2}}c{{m}^{3}}.$
D. $2500{{\pi }^{2}}c{{m}^{3}}.$

Cách 1: Thiết diện ngang của săm là hình tròn có bán kính $R={{R}_{2}}-{{R}_{1}}=5cm.$ Chọn hệ trục tọa độ có gốc trùng với tâm O của các đường tròn, khi thiết diện ngang của săm sẽ là đường tròn tâm $I\left( 0;25 \right)$ và bán kính $R=5.$
Ta có phương trình đường tròn:
${{x}^{2}}+{{\left( y-25 \right)}^{2}}=25\Leftrightarrow {{\left( y-25 \right)}^{2}}=25-{{x}^{2}}\Leftrightarrow \left[ \begin{aligned}
& y=25+\sqrt{25-{{x}^{2}}} \\
& y=25-\sqrt{25-{{x}^{2}}} \\
\end{aligned} \right.$
Thể tích khối tròn xoay sinh ra khi quay hình tròn trên quanh trục Ox là:
$V=\pi \int\limits_{-5}^{5}{\left[ {{\left( 25+\sqrt{25-{{x}^{2}}} \right)}^{2}}-{{\left( 25-\sqrt{25-{{x}^{2}}} \right)}^{2}}dx \right]}=100\pi \int\limits_{-5}^{5}{\sqrt{25-{{x}^{2}}}dx}$
Đặt $x=5\sin t,t\in \left[ \dfrac{-\pi }{2};\dfrac{\pi }{2} \right]$ thì $V=100\pi \int\limits_{-\dfrac{\pi }{2}}^{\dfrac{\pi }{2}}{25{{\cos }^{2}}tdt}=1250{{\pi }^{2}}\left( c{{m}^{3}} \right).$
Cách 2: Theo công thức thể tích hình khuyên:
$V=\dfrac{1}{4}{{\pi }^{2}}\left( {{R}_{2}}+{{R}_{1}} \right){{\left( {{R}_{2}}-{{R}_{1}} \right)}^{2}}=\dfrac{1}{4}{{\pi }^{2}}\left( 30+20 \right){{\left( 30-20 \right)}^{2}}=1250{{\pi }^{2}}\left( c{{m}^{3}} \right).$

A. $600{{\pi }^{2}}c{{m}^{3}}.$
B. $1400\pi c{{m}^{3}}.$
C. $1250{{\pi }^{2}}c{{m}^{3}}.$
D. $2500{{\pi }^{2}}c{{m}^{3}}.$
Cách 1: Thiết diện ngang của săm là hình tròn có bán kính $R={{R}_{2}}-{{R}_{1}}=5cm.$ Chọn hệ trục tọa độ có gốc trùng với tâm O của các đường tròn, khi thiết diện ngang của săm sẽ là đường tròn tâm $I\left( 0;25 \right)$ và bán kính $R=5.$
Ta có phương trình đường tròn:
${{x}^{2}}+{{\left( y-25 \right)}^{2}}=25\Leftrightarrow {{\left( y-25 \right)}^{2}}=25-{{x}^{2}}\Leftrightarrow \left[ \begin{aligned}
& y=25+\sqrt{25-{{x}^{2}}} \\
& y=25-\sqrt{25-{{x}^{2}}} \\
\end{aligned} \right.$
Thể tích khối tròn xoay sinh ra khi quay hình tròn trên quanh trục Ox là:
$V=\pi \int\limits_{-5}^{5}{\left[ {{\left( 25+\sqrt{25-{{x}^{2}}} \right)}^{2}}-{{\left( 25-\sqrt{25-{{x}^{2}}} \right)}^{2}}dx \right]}=100\pi \int\limits_{-5}^{5}{\sqrt{25-{{x}^{2}}}dx}$
Đặt $x=5\sin t,t\in \left[ \dfrac{-\pi }{2};\dfrac{\pi }{2} \right]$ thì $V=100\pi \int\limits_{-\dfrac{\pi }{2}}^{\dfrac{\pi }{2}}{25{{\cos }^{2}}tdt}=1250{{\pi }^{2}}\left( c{{m}^{3}} \right).$
Cách 2: Theo công thức thể tích hình khuyên:
$V=\dfrac{1}{4}{{\pi }^{2}}\left( {{R}_{2}}+{{R}_{1}} \right){{\left( {{R}_{2}}-{{R}_{1}} \right)}^{2}}=\dfrac{1}{4}{{\pi }^{2}}\left( 30+20 \right){{\left( 30-20 \right)}^{2}}=1250{{\pi }^{2}}\left( c{{m}^{3}} \right).$
Đáp án C.