Biết hàm số $f(x)=\left\{\begin{array}{lll}x^2+3 & \text { khi } &...

Tập xác định: $D=\mathbb{R}$.
Với $x>1$ ta có $f(x)=x^2+3$ xác định và liên tục trên khoảng $(1 ;+\infty)$.
Với $x<1$ ta có $f(x)=5-x+2021 a$ xác định và liên tục trên khoảng $(-\infty ; 1)$.
Xét tại $x=1$ ta có $\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{+}}\left(x^2+3\right)=4$.
$
\begin{aligned}
& \lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}}(5-x+2021 a)=4+2021 a . \\
& \text { Và } f(1)=4 .
\end{aligned}
$
Vậy để hàm số $f(x)$ liên tục trên tập thì $f(x)$ phải liên tục tại điểm $x=1$
$
\Leftrightarrow \lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{-}} f(x)=f(1) \Leftrightarrow 4=4+2021 a \Leftrightarrow a=0
$
Khi đó $f(x)=\left\{\begin{array}{lll}x^2+3 & \text { khi } & x \geq 1 \\ 5-x & \text { khi } & x<1\end{array}\right.$.
Xét tích phân $I_1=\int_0^{\dfrac{\pi}{2}} f(\sin x) \cos x \mathrm{~d} x$.Đặt $t=\sin x \Rightarrow \mathrm{d} t=\cos x \mathrm{~d} x$.
Đổi cận
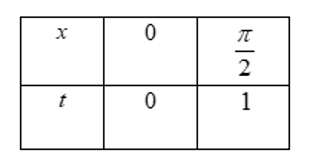Ta có $I_1=\int_0^1 f(t) \mathrm{d} t=\int_0^1 f(x) \mathrm{d} x=\int_0^1(5-x) \mathrm{d} x=\left.\left(5 x-\dfrac{x^2}{2}\right)\right|_0 ^1=\dfrac{9}{2}$
Xét tích phân $I_2=\int_0^1 f(3-2 x) \mathrm{d} x$. Đặt $t=3-2 x \Rightarrow \mathrm{d} t=-2 \mathrm{~d} x \Rightarrow \mathrm{d} x=\dfrac{-\mathrm{d} t}{2}$.
Đổi cận
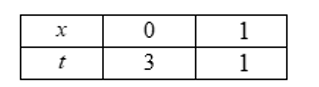Ta có $I_2=\int_0^1 f(3-2 x) \mathrm{d} x=-\dfrac{1}{2} \int_3^1 f(t) \mathrm{d} t=\dfrac{1}{2} \int_1^3 f(t) \mathrm{d} t=\dfrac{1}{2} \int_1^3 f(x) \mathrm{d} x=\dfrac{1}{2} \int_1^3\left(x^2+3\right) \mathrm{d} x$ $=\left.\dfrac{1}{2}\left(\dfrac{x^3}{3}+3 x\right)\right|_1 ^3=\dfrac{1}{2}\left(18-\dfrac{10}{3}\right)=\dfrac{22}{3}$.
Vậy $I=2 \int_0^{\dfrac{\pi}{2}} f(\sin x) \cos x \mathrm{~d} x+3 \int_0^1 f(3-2 x) \mathrm{d} x=9+22=31$.