Câu hỏi: Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?
Phương pháp giải
- Đặt ẩn x, y và đặt điiều kiện
- Biểu diễn các ẩn số thông qua dữ liệu đề bài cho
- Giải hệ bất phương trình vừa lập được
- Kết luận
Lời giải chi tiết
Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 \({m^2}\)), điều kiện \(x \ge 0, y \ge 0\), ta có \(x + y \le 8\).
Số công cần dùng là \(20x + 30y \le 180\) hay \(2x + 3y \le 18\).
Số tiền thu được là
\(F = 3000000x + 4000000y\)(đồng)
Hay \(F = 3x + 4y\) (triệu đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x + y \le 8\\2x + 3y \le 18\\x \ge 0\\y \ge 0\end{array} \right.\)
Sao cho \(F = 3x + 4y\) đạt giá trị lớn nhất.
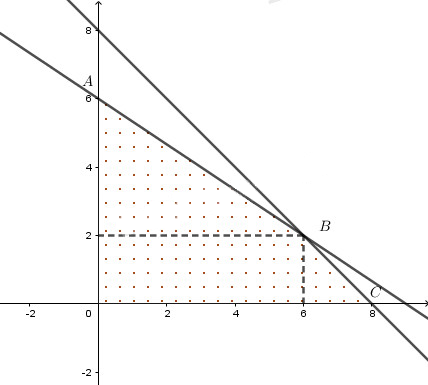
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0; 6), B(6; 2), C(8; 0) và O(0; 0).
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra \(x = 6, y = 2\) (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6(a) đậu, 2(a) cà, thu hoạch 26 000 000 đồng.
- Đặt ẩn x, y và đặt điiều kiện
- Biểu diễn các ẩn số thông qua dữ liệu đề bài cho
- Giải hệ bất phương trình vừa lập được
- Kết luận
Lời giải chi tiết
Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 \({m^2}\)), điều kiện \(x \ge 0, y \ge 0\), ta có \(x + y \le 8\).
Số công cần dùng là \(20x + 30y \le 180\) hay \(2x + 3y \le 18\).
Số tiền thu được là
\(F = 3000000x + 4000000y\)(đồng)
Hay \(F = 3x + 4y\) (triệu đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x + y \le 8\\2x + 3y \le 18\\x \ge 0\\y \ge 0\end{array} \right.\)
Sao cho \(F = 3x + 4y\) đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0; 6), B(6; 2), C(8; 0) và O(0; 0).
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra \(x = 6, y = 2\) (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6(a) đậu, 2(a) cà, thu hoạch 26 000 000 đồng.