Câu hỏi: Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} neu x \ge 0\\{x^2} - 1 neu x < 0\end{array} \right.\)
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = {x^2}\) và \(y = {x^2} - 1\) trên cùng một hệ trục tọa độ.
Khi \(x \ge 0\) thì \(f\left( x \right) = {x^2}\) nên xóa nhánh đồ thị \(y = {x^2}\) bên trái trục tung đi.
Khi \(x < 0\) thì \(f\left( x \right) = {x^2} - 1\) nên xóa nhánh đồ thị \(y = {x^2} - 1\) bên phải trục tung đi.
Ta được đồ thị hàm số \(y = f\left( x \right)\).
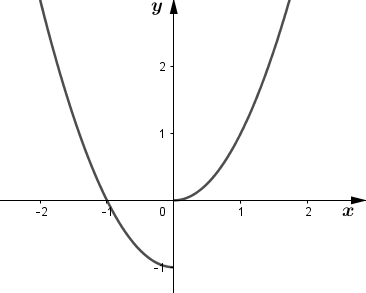
Từ đồ thị ta thấy hàm số không có giới hạn khi \(x \to 0\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Lấy dãy \(\left\{ {{x_n}} \right\}\) và \(\left\{ {{y_n}} \right\}\) thỏa mãn \({x_n} = \dfrac{1}{n}\) và \({y_n} = - \dfrac{1}{n}\)
Dễ thấy \(\lim {x_n} = 0,\lim {y_n} = 0\).
Ta có:
Vì \({x_n} = \dfrac{1}{n} > 0\) nên \(\lim f\left( {{x_n}} \right) = \lim x_n^2 = \lim \dfrac{1}{{{n^2}}} = 0\)
Vì \({y_n} = - \dfrac{1}{n} < 0\) nên \(\lim f\left( {{y_n}} \right) = \lim \left({y_n^2 - 1} \right)\)\(= \lim \left[ {{{\left( { - \dfrac{1}{n}} \right)}^2} - 1} \right]\) \(= \lim \left[ {\dfrac{1}{{{n^2}}} - 1} \right] = 0 - 1 = - 1\)
Do \(\lim f\left( {{x_n}} \right) \ne \lim f\left({{y_n}} \right)\) nên không tồn tại giới hạn hàm số khi \(x \to 0\).
Câu a
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = {x^2}\) và \(y = {x^2} - 1\) trên cùng một hệ trục tọa độ.
Khi \(x \ge 0\) thì \(f\left( x \right) = {x^2}\) nên xóa nhánh đồ thị \(y = {x^2}\) bên trái trục tung đi.
Khi \(x < 0\) thì \(f\left( x \right) = {x^2} - 1\) nên xóa nhánh đồ thị \(y = {x^2} - 1\) bên phải trục tung đi.
Ta được đồ thị hàm số \(y = f\left( x \right)\).

Từ đồ thị ta thấy hàm số không có giới hạn khi \(x \to 0\).
Câu b
b) Dùng định nghĩa chứng minh dự đoán trên.Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Lấy dãy \(\left\{ {{x_n}} \right\}\) và \(\left\{ {{y_n}} \right\}\) thỏa mãn \({x_n} = \dfrac{1}{n}\) và \({y_n} = - \dfrac{1}{n}\)
Dễ thấy \(\lim {x_n} = 0,\lim {y_n} = 0\).
Ta có:
Vì \({x_n} = \dfrac{1}{n} > 0\) nên \(\lim f\left( {{x_n}} \right) = \lim x_n^2 = \lim \dfrac{1}{{{n^2}}} = 0\)
Vì \({y_n} = - \dfrac{1}{n} < 0\) nên \(\lim f\left( {{y_n}} \right) = \lim \left({y_n^2 - 1} \right)\)\(= \lim \left[ {{{\left( { - \dfrac{1}{n}} \right)}^2} - 1} \right]\) \(= \lim \left[ {\dfrac{1}{{{n^2}}} - 1} \right] = 0 - 1 = - 1\)
Do \(\lim f\left( {{x_n}} \right) \ne \lim f\left({{y_n}} \right)\) nên không tồn tại giới hạn hàm số khi \(x \to 0\).
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!