Câu hỏi: Chứng minh rằng nếu tứ diện ABCD có \(AB \bot C{\rm{D}}\) và \(AC \bot B{\rm{D}}\) thì \(AD \bot BC\).
Phương pháp giải
Sử dụng lý thuyết: "Một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó."
Lời giải chi tiết
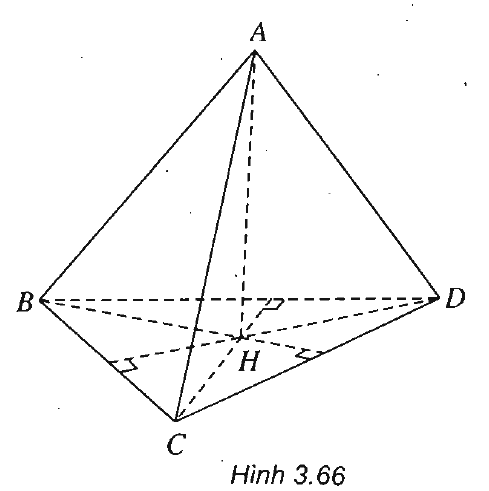
Vẽ \(AH \bot \left( {BC{\rm{D}}} \right)\) tại H, ta có \(C{\rm{D}} \bot AH\) và vì \(C{\rm{D}} \bot AB\) ta suy ra \(C{\rm{D}} \bot BH\). Tương tự vì \({\rm{BD}} \bot AC\) ta suy ra \({\rm{BD}} \bot CH\)
Vậy H là trực tâm của tam giác BCD tức là \(DH \bot BC\)
Vì \(AH \bot BC\) nên ta suy ra \(BC \bot A{\rm{D}}\)
Cách khác . Trước hết ta hãy chứng minh hệ thức:
\(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = 0\) với bốn điểm A, B, C, D bất kì.
Thực vậy, ta có:
\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = \overrightarrow {AB} .\left({\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} .\overrightarrow {AB} \left(1 \right) \cr
& \overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} .\left({\overrightarrow {AB} - \overrightarrow {{\rm{AD}}} } \right) = \overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {{\rm{AD}}} \left(2 \right) \cr
& \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = \overrightarrow {{\rm{AD}}} .\left({\overrightarrow {AC} - \overrightarrow {AB} } \right) = \overrightarrow {{\rm{AD}}} .\overrightarrow {AC} - \overrightarrow {{\rm{AD}}} .\overrightarrow {AB} \left(3 \right) \cr} \)
\(\left( 1 \right) + \left(2 \right) + \left(3 \right) \Leftrightarrow \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0 \left(4 \right)\)
Do đó nếu \(AB \bot CD\) nghĩa là \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = 0 \), \(AC \bot BD\) nghĩa là \(\overrightarrow {AC} .\overrightarrow {B{\rm{D}}} = 0 \)
Từ hệ thức (4) ta suy ra \(\overrightarrow {AD} .\overrightarrow {BC} = 0 \), do đó \(A{\rm{D}} \bot BC\).
Sử dụng lý thuyết: "Một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó."
Lời giải chi tiết
Vẽ \(AH \bot \left( {BC{\rm{D}}} \right)\) tại H, ta có \(C{\rm{D}} \bot AH\) và vì \(C{\rm{D}} \bot AB\) ta suy ra \(C{\rm{D}} \bot BH\). Tương tự vì \({\rm{BD}} \bot AC\) ta suy ra \({\rm{BD}} \bot CH\)
Vậy H là trực tâm của tam giác BCD tức là \(DH \bot BC\)
Vì \(AH \bot BC\) nên ta suy ra \(BC \bot A{\rm{D}}\)
Cách khác . Trước hết ta hãy chứng minh hệ thức:
\(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = 0\) với bốn điểm A, B, C, D bất kì.
Thực vậy, ta có:
\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = \overrightarrow {AB} .\left({\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} .\overrightarrow {AB} \left(1 \right) \cr
& \overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} .\left({\overrightarrow {AB} - \overrightarrow {{\rm{AD}}} } \right) = \overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {{\rm{AD}}} \left(2 \right) \cr
& \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = \overrightarrow {{\rm{AD}}} .\left({\overrightarrow {AC} - \overrightarrow {AB} } \right) = \overrightarrow {{\rm{AD}}} .\overrightarrow {AC} - \overrightarrow {{\rm{AD}}} .\overrightarrow {AB} \left(3 \right) \cr} \)
\(\left( 1 \right) + \left(2 \right) + \left(3 \right) \Leftrightarrow \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0 \left(4 \right)\)
Do đó nếu \(AB \bot CD\) nghĩa là \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = 0 \), \(AC \bot BD\) nghĩa là \(\overrightarrow {AC} .\overrightarrow {B{\rm{D}}} = 0 \)
Từ hệ thức (4) ta suy ra \(\overrightarrow {AD} .\overrightarrow {BC} = 0 \), do đó \(A{\rm{D}} \bot BC\).