Câu hỏi: Cho tam giác đều \(ACB\) và \(ACD,\) cạnh \(a.\) Lần lượt lấy \(B\) và \(D\) làm tâm vẽ hai đường tròn bán kính \(a.\) Kẻ các đường kính \(ABE\) và \(ADF.\) Trên cung nhỏ \(CE\) của đường tròn tâm \(B\) lấy điểm \(M\) (không trùng với \(E\) và \(C\)). Đường thẳng \(CM\) cắt đường tròn tâm \(D\) tại điểm thứ hai là \(N.\) Hai đường thẳng \(EM\) và \(NF\) cắt nhau tại điểm \(T.\) Gọi \(H\) là giao điểm của \(AT\) và \(MN.\) Chứng minh:
\(a)\) \(MNT\) là tam giác đều.
\(b)\) \(AT = 4AH.\)
\(a)\) \(MNT\) là tam giác đều.
\(b)\) \(AT = 4AH.\)
Phương pháp giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
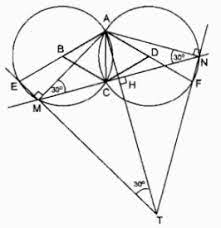
\(a)\) Trong đường tròn \((B)\) ta có:
\(\widehat {AMC} = \displaystyle {1 \over 2}\widehat {ABC}\) (hệ quả góc nội tiếp) mà \(\widehat {ABC} = 60^\circ \) (vì \(∆ABC\) đều)
\( \Rightarrow \widehat {AMC} = 30^\circ \)
\(\widehat {AME} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \((B)\))
\( \Rightarrow \widehat {AMT} = 90^\circ \)
\(\widehat {TMN} = \widehat {AMT} - \widehat {AMC}\)\( = 90^\circ - 30^\circ = 60^\circ \)
Trong đường tròn \((D)\) ta có:
\(\widehat {ANC} =\displaystyle{1 \over 2}\widehat {ADC}\) (Hệ quả góc nội tiếp) mà \(\widehat {ADC} = 60^\circ \) (vì \(∆ADC\) đều) \( \Rightarrow \widehat {ANC} = 30^\circ \)
\(\widehat {ANF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \((D)\))
\( \Rightarrow \widehat {ANC} + \widehat {CNF} = 90^\circ\)
\( \Rightarrow \widehat {CNF} = 90^\circ - \widehat {ANC}\)\( = 90^\circ - 30^\circ = 60^\circ \) hay \(\widehat {MNT} = 60^\circ \)
Vậy \(∆TMN\) đều.
\(b)\) \(\widehat {AMC} = \widehat {ANC} = 30^\circ \) (theo câu a)
\( \Rightarrow \Delta AMN\) cân tại \(A\) \( \Rightarrow AM = AN\) nên \(A\) nằm trên đường trung trực \(MN\)
Vì \(∆TMN\) đều \( \Rightarrow TM = TN\) nên \(T\) nằm trên đường trung trực \(MN\)
Suy ra \(AT\) là đường trung trực của \(MN\) nên \(AT ⊥ MN\)
\(∆AHM\) có \(\widehat {AHM} = 90^\circ \)
\(AM =\displaystyle{{AH} \over {\sin M}} = {{AH} \over {\sin 30^\circ }}\)\( =\displaystyle {{AH} \over {\displaystyle{1 \over 2}}} = 2AH\) \( (1)\)
Vì \(∆TMN\) đều có \(TH ⊥ MN\) nên \(TH\) cũng là đường phân giác của \(\widehat T\) nên \(\widehat {MTA} = 30^\circ \)
\(∆AMT\) có \(\widehat {AMT} = 90^\circ \)
\(AT = \displaystyle{{AM} \over {\sin \widehat {MTA}}} = {\displaystyle{AM} \over {\displaystyle{1 \over 2}}} = 2AM\)\( (2)\)
Từ \((1)\) và \((2)\) suy ra: \(AT =2AM=2.2AH= 4AH\)
Vậy \(AT=4AH.\)
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
\(a)\) Trong đường tròn \((B)\) ta có:
\(\widehat {AMC} = \displaystyle {1 \over 2}\widehat {ABC}\) (hệ quả góc nội tiếp) mà \(\widehat {ABC} = 60^\circ \) (vì \(∆ABC\) đều)
\( \Rightarrow \widehat {AMC} = 30^\circ \)
\(\widehat {AME} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \((B)\))
\( \Rightarrow \widehat {AMT} = 90^\circ \)
\(\widehat {TMN} = \widehat {AMT} - \widehat {AMC}\)\( = 90^\circ - 30^\circ = 60^\circ \)
Trong đường tròn \((D)\) ta có:
\(\widehat {ANC} =\displaystyle{1 \over 2}\widehat {ADC}\) (Hệ quả góc nội tiếp) mà \(\widehat {ADC} = 60^\circ \) (vì \(∆ADC\) đều) \( \Rightarrow \widehat {ANC} = 30^\circ \)
\(\widehat {ANF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \((D)\))
\( \Rightarrow \widehat {ANC} + \widehat {CNF} = 90^\circ\)
\( \Rightarrow \widehat {CNF} = 90^\circ - \widehat {ANC}\)\( = 90^\circ - 30^\circ = 60^\circ \) hay \(\widehat {MNT} = 60^\circ \)
Vậy \(∆TMN\) đều.
\(b)\) \(\widehat {AMC} = \widehat {ANC} = 30^\circ \) (theo câu a)
\( \Rightarrow \Delta AMN\) cân tại \(A\) \( \Rightarrow AM = AN\) nên \(A\) nằm trên đường trung trực \(MN\)
Vì \(∆TMN\) đều \( \Rightarrow TM = TN\) nên \(T\) nằm trên đường trung trực \(MN\)
Suy ra \(AT\) là đường trung trực của \(MN\) nên \(AT ⊥ MN\)
\(∆AHM\) có \(\widehat {AHM} = 90^\circ \)
\(AM =\displaystyle{{AH} \over {\sin M}} = {{AH} \over {\sin 30^\circ }}\)\( =\displaystyle {{AH} \over {\displaystyle{1 \over 2}}} = 2AH\) \( (1)\)
Vì \(∆TMN\) đều có \(TH ⊥ MN\) nên \(TH\) cũng là đường phân giác của \(\widehat T\) nên \(\widehat {MTA} = 30^\circ \)
\(∆AMT\) có \(\widehat {AMT} = 90^\circ \)
\(AT = \displaystyle{{AM} \over {\sin \widehat {MTA}}} = {\displaystyle{AM} \over {\displaystyle{1 \over 2}}} = 2AM\)\( (2)\)
Từ \((1)\) và \((2)\) suy ra: \(AT =2AM=2.2AH= 4AH\)
Vậy \(AT=4AH.\)