Câu hỏi: Cho tứ diện \(ABCD\). Trên ba cạnh \(AB, AC, AD\) lần lượt lấy các điểm \(B’, C’, D’\) sao cho đường thẳng \(B’C’\) cắt đường thẳng \(BC\) tại \(K\), đường thẳng \(C’D’\) cắt đường thẳng \(CD\) tại \(J\), đường thẳng \(D’B’\) cắt đường thẳng \(DB\) tại \(I\).
a) Chứng minh ba điểm \(I, J, K\) thẳng hàng.
b) Lấy điểm \(M\) ở giữa đoạn thẳng \(BD\); điểm \(N\) ở giữa đoạn thẳng \(CD\) sao cho đường thẳng \(MN\) cắt đường thẳng \(BC\) và điểm \(F\) nằm bên trong tam giác \(ABC\). Xác định thiết diện của tứ diện \(ABCD\) khi cắt bởi mặt phẳng \((MNF)\).
a) Chứng minh ba điểm \(I, J, K\) thẳng hàng.
b) Lấy điểm \(M\) ở giữa đoạn thẳng \(BD\); điểm \(N\) ở giữa đoạn thẳng \(CD\) sao cho đường thẳng \(MN\) cắt đường thẳng \(BC\) và điểm \(F\) nằm bên trong tam giác \(ABC\). Xác định thiết diện của tứ diện \(ABCD\) khi cắt bởi mặt phẳng \((MNF)\).
Phương pháp giải
a) Chứng minh ba điểm \(I, J, K\) cùng thuộc giao tuyến của \((CBD)\) và \((C’B’D’)\).
b) Xác định giao tuyến của mặt phẳng \((MNF)\) với các mặt của \(ABCD\).
Lời giải chi tiết
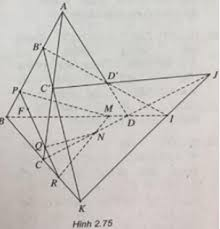
A) Ta có:
\(K = B'C' \cap BC\)\(\Rightarrow \left\{ \begin{array}{l}K \in B'C' \subset \left( {B'C'D'} \right)\\K \in BC \subset \left({BCD} \right)\end{array} \right.\) \(\Rightarrow K \in \left( {B'C'D'} \right) \cap \left({BCD} \right)\)
\(J = C'D' \cap CD\)\(\Rightarrow \left\{ \begin{array}{l}J \in C'D' \subset \left( {B'C'D'} \right)\\J \in CD \subset \left({BCD} \right)\end{array} \right.\) \(\Rightarrow J \in \left( {B'C'D'} \right) \cap \left({BCD} \right)\)
Do đó \(KJ = \left( {B'C'D'} \right) \cap \left({BCD} \right)\).
Mà \(I = B'D' \cap BD\)\(\Rightarrow \left\{ \begin{array}{l}I \in B'D' \subset \left( {B'C'D'} \right)\\I \in BD \subset \left({BCD} \right)\end{array} \right.\) \(\Rightarrow I \in \left( {B'C'D'} \right) \cap \left({BCD} \right) = KJ\)
Vậy ba điểm I, J, K thẳng hàng.
b) Trong (BCD), gọi \(R = MN \cap BC\).
Trong (ABC), gọi \(P, Q\) lần lượt là giao điểm của RF với AB, AC.
Khi đó
\(\begin{array}{l}\left( {MNF} \right) \cap \left({BCD} \right) = MN\\\left({MNF} \right) \cap \left({ACD} \right) = NQ\\\left({MNF} \right) \cap \left({ABC} \right) = QP\\\left({MNF} \right) \cap \left({ABD} \right) = PM\end{array}\)
Vật thiết diện là tứ giác MNQP.
a) Chứng minh ba điểm \(I, J, K\) cùng thuộc giao tuyến của \((CBD)\) và \((C’B’D’)\).
b) Xác định giao tuyến của mặt phẳng \((MNF)\) với các mặt của \(ABCD\).
Lời giải chi tiết
A) Ta có:
\(K = B'C' \cap BC\)\(\Rightarrow \left\{ \begin{array}{l}K \in B'C' \subset \left( {B'C'D'} \right)\\K \in BC \subset \left({BCD} \right)\end{array} \right.\) \(\Rightarrow K \in \left( {B'C'D'} \right) \cap \left({BCD} \right)\)
\(J = C'D' \cap CD\)\(\Rightarrow \left\{ \begin{array}{l}J \in C'D' \subset \left( {B'C'D'} \right)\\J \in CD \subset \left({BCD} \right)\end{array} \right.\) \(\Rightarrow J \in \left( {B'C'D'} \right) \cap \left({BCD} \right)\)
Do đó \(KJ = \left( {B'C'D'} \right) \cap \left({BCD} \right)\).
Mà \(I = B'D' \cap BD\)\(\Rightarrow \left\{ \begin{array}{l}I \in B'D' \subset \left( {B'C'D'} \right)\\I \in BD \subset \left({BCD} \right)\end{array} \right.\) \(\Rightarrow I \in \left( {B'C'D'} \right) \cap \left({BCD} \right) = KJ\)
Vậy ba điểm I, J, K thẳng hàng.
b) Trong (BCD), gọi \(R = MN \cap BC\).
Trong (ABC), gọi \(P, Q\) lần lượt là giao điểm của RF với AB, AC.
Khi đó
\(\begin{array}{l}\left( {MNF} \right) \cap \left({BCD} \right) = MN\\\left({MNF} \right) \cap \left({ACD} \right) = NQ\\\left({MNF} \right) \cap \left({ABC} \right) = QP\\\left({MNF} \right) \cap \left({ABD} \right) = PM\end{array}\)
Vật thiết diện là tứ giác MNQP.