Câu hỏi: Tính thể tích khối tứ diện đều cạnh \(a\).
Phương pháp giải
+) Gọi \(AH\) là đường cao hạ từ đỉnh A của tứ diện đều \(ABCD\) \(\left({H \in (BCD)} \right)\).
+) Do tứ diện ABCD đều, chứng minh H là trọng tâm tam giác \(ABC\).
+) Sử dụng định lí Pytago tính độ dài \(AH\).
+) Áp dụng công thức tính thể tích: \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}}\).
Lời giải chi tiết
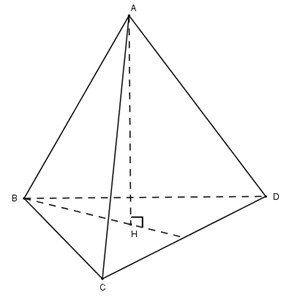
Cho tứ diện đều \(ABCD\). Hạ \(AH \bot \left( {BCD} \right)\)
Dễ dàng chứng minh được \({\Delta _v}AHB = {\Delta _v}AHC = {\Delta _v}AHD \left( {ch - cgv} \right) \) \(\Rightarrow HB = HC = HD,\) do đó H là tâm đường tròn ngoại tiếp tam giác \(BCD\).
Do \(BCD\) là tam giác đều nên \(H\) là trọng tâm của tam giác \(BCD\).
Gọi M là trung điểm CD thì BM vừa là trung tuyến vừa là đường cao trong tam giác.
Ta có: \(BM = BD\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)
Do đó \(BH = \frac{2}{3}BM= \displaystyle{2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a\)
Áp dụng định lí Pitago trong tam giác vuông \(ABH\) ta có: \(A{H^2} = A{B^2} - B{H^2} = {a^2} - \dfrac{{{a^2}}}{3} = \dfrac{{2{a^2}}}{3} \) \(\Rightarrow AH = \dfrac{{a\sqrt 6 }}{3}\)
Do tam giác \(BCD\) đều cạnh \(a\) nên: \({S_{BCD}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}} \) \(= \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} \) \(= \dfrac{{{a^3}\sqrt 2 }}{{12}}.\)
+) Gọi \(AH\) là đường cao hạ từ đỉnh A của tứ diện đều \(ABCD\) \(\left({H \in (BCD)} \right)\).
+) Do tứ diện ABCD đều, chứng minh H là trọng tâm tam giác \(ABC\).
+) Sử dụng định lí Pytago tính độ dài \(AH\).
+) Áp dụng công thức tính thể tích: \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}}\).
Lời giải chi tiết
Cho tứ diện đều \(ABCD\). Hạ \(AH \bot \left( {BCD} \right)\)
Dễ dàng chứng minh được \({\Delta _v}AHB = {\Delta _v}AHC = {\Delta _v}AHD \left( {ch - cgv} \right) \) \(\Rightarrow HB = HC = HD,\) do đó H là tâm đường tròn ngoại tiếp tam giác \(BCD\).
Do \(BCD\) là tam giác đều nên \(H\) là trọng tâm của tam giác \(BCD\).
Gọi M là trung điểm CD thì BM vừa là trung tuyến vừa là đường cao trong tam giác.
Ta có: \(BM = BD\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)
Do đó \(BH = \frac{2}{3}BM= \displaystyle{2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a\)
Áp dụng định lí Pitago trong tam giác vuông \(ABH\) ta có: \(A{H^2} = A{B^2} - B{H^2} = {a^2} - \dfrac{{{a^2}}}{3} = \dfrac{{2{a^2}}}{3} \) \(\Rightarrow AH = \dfrac{{a\sqrt 6 }}{3}\)
Do tam giác \(BCD\) đều cạnh \(a\) nên: \({S_{BCD}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}} \) \(= \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} \) \(= \dfrac{{{a^3}\sqrt 2 }}{{12}}.\)