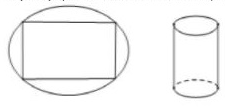
Câu hỏi: Từ một tâm tôn có hình dạng là một Elip với độ dài trục lớn bằng 8, độ dài trục bé bằng 4, ta cắt lấy tấm tôn có dạng hình chữ nhật nội tiếp Elip (tham khảo hình vẽ sau). Gõ tấm tôn hình chữ nhật thu được thành một hình trụ không có đáy.
Thể tích lớn nhất của khối trụ giới hạn bởi hình trụ trên bằng:
A. $\dfrac{128}{3\sqrt{2}\pi }$
B. $\dfrac{64\sqrt{3}}{9\pi }$
C. $\dfrac{64}{3\sqrt{2}\pi }$
D. $\dfrac{128\sqrt{3}}{9\pi }$

Thể tích lớn nhất của khối trụ giới hạn bởi hình trụ trên bằng:
A. $\dfrac{128}{3\sqrt{2}\pi }$
B. $\dfrac{64\sqrt{3}}{9\pi }$
C. $\dfrac{64}{3\sqrt{2}\pi }$
D. $\dfrac{128\sqrt{3}}{9\pi }$
Phương pháp:
- Lập phương trình Elip.
- Giả sử hình chữ nhật có chiều dài $2a\left( 0<a<4 \right).$ Khi đó chu vi đáy hình trụ bằng $2a,$ tính bán kính đáy của hình trụ.
- Tính chiều cao hình trụ.
- Thể tích khối trụ có chiều cao $h,$ bán kính đáy $r$ là $V=\pi {{r}^{2}}h.$
- Sử dụng phương pháp hàm số để tìm GTLN của hàm số.
Cách giải:
Theo bài ra ta có $\left\{ \begin{aligned}
& 2a=8 \\
& 2b=4 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=4 \\
& b=2 \\
\end{aligned} \right.\Rightarrow $ Phương trình elip là: $ \dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1\left( E \right).$
Giả sử hình chữ nhật có chiều dài $2a\left( 0<a<4 \right).$ Khi đó chu vi đáy hình trụ bằng $2a,$ nên bán kính đáy là $R=\dfrac{2a}{2\pi }=\dfrac{a}{\pi }.$
Đặt hệ trục tọa độ như hình vẽ

Thay $x=a$ ta có $\dfrac{{{a}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1\Leftrightarrow {{y}^{2}}=4\left( 1-\dfrac{{{a}^{2}}}{16} \right)\Rightarrow {{y}_{A}}=2\sqrt{1-\dfrac{{{a}^{2}}}{16}}\Rightarrow A\left( a;2\sqrt{1-\dfrac{{{a}^{2}}}{16}} \right)$.
$\Rightarrow $ Chiều rộng của hình chữ nhật là $4\sqrt{1-\dfrac{{{a}^{2}}}{16}}\Rightarrow $ Chiều cao của hình trụ là $h=4\sqrt{1-\dfrac{{{a}^{2}}}{16}}.$
$\Rightarrow $ Thể tích khối trụ: $V=\pi {{R}^{2}}h=\pi .\dfrac{{{a}^{2}}}{\pi }4\sqrt{1-\dfrac{{{a}^{2}}}{16}}=\dfrac{64}{\pi }.\dfrac{{{a}^{2}}}{16}\sqrt{1-\dfrac{{{a}^{2}}}{16}}.$
Xét hàm số $f\left( a \right)=\dfrac{{{a}^{2}}}{16}\sqrt{1-\dfrac{{{a}^{2}}}{16}}$, đặt $t=\dfrac{{{a}^{2}}}{16}\left( 0<t<1 \right)\Rightarrow f\left( t \right)=t\sqrt{1-t}.$
Ta có
$f'\left( t \right)=\sqrt{1-t}+t.\dfrac{-1}{2\sqrt{1-t}}=\dfrac{2-3t}{2\sqrt{1-t}}$
$f'\left( t \right)=0\Leftrightarrow 2-3t=0\Leftrightarrow t=\dfrac{2}{3}$
$\Rightarrow \underset{\left( 0;1 \right)}{\mathop{\max }} f\left( t \right)=f\left( \dfrac{2}{3} \right)=\dfrac{2}{3}.\sqrt{1-\dfrac{2}{3}}=\dfrac{2\sqrt{3}}{9}.$
Vậy thể tích lớn nhất của khối trụ giới hạn bởi hình trụ trên bằng $\dfrac{64}{\pi }.\dfrac{2\sqrt{3}}{9}=\dfrac{128\sqrt{3}}{9\pi }.$
- Lập phương trình Elip.
- Giả sử hình chữ nhật có chiều dài $2a\left( 0<a<4 \right).$ Khi đó chu vi đáy hình trụ bằng $2a,$ tính bán kính đáy của hình trụ.
- Tính chiều cao hình trụ.
- Thể tích khối trụ có chiều cao $h,$ bán kính đáy $r$ là $V=\pi {{r}^{2}}h.$
- Sử dụng phương pháp hàm số để tìm GTLN của hàm số.
Cách giải:
Theo bài ra ta có $\left\{ \begin{aligned}
& 2a=8 \\
& 2b=4 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=4 \\
& b=2 \\
\end{aligned} \right.\Rightarrow $ Phương trình elip là: $ \dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1\left( E \right).$
Giả sử hình chữ nhật có chiều dài $2a\left( 0<a<4 \right).$ Khi đó chu vi đáy hình trụ bằng $2a,$ nên bán kính đáy là $R=\dfrac{2a}{2\pi }=\dfrac{a}{\pi }.$
Đặt hệ trục tọa độ như hình vẽ
Thay $x=a$ ta có $\dfrac{{{a}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1\Leftrightarrow {{y}^{2}}=4\left( 1-\dfrac{{{a}^{2}}}{16} \right)\Rightarrow {{y}_{A}}=2\sqrt{1-\dfrac{{{a}^{2}}}{16}}\Rightarrow A\left( a;2\sqrt{1-\dfrac{{{a}^{2}}}{16}} \right)$.
$\Rightarrow $ Chiều rộng của hình chữ nhật là $4\sqrt{1-\dfrac{{{a}^{2}}}{16}}\Rightarrow $ Chiều cao của hình trụ là $h=4\sqrt{1-\dfrac{{{a}^{2}}}{16}}.$
$\Rightarrow $ Thể tích khối trụ: $V=\pi {{R}^{2}}h=\pi .\dfrac{{{a}^{2}}}{\pi }4\sqrt{1-\dfrac{{{a}^{2}}}{16}}=\dfrac{64}{\pi }.\dfrac{{{a}^{2}}}{16}\sqrt{1-\dfrac{{{a}^{2}}}{16}}.$
Xét hàm số $f\left( a \right)=\dfrac{{{a}^{2}}}{16}\sqrt{1-\dfrac{{{a}^{2}}}{16}}$, đặt $t=\dfrac{{{a}^{2}}}{16}\left( 0<t<1 \right)\Rightarrow f\left( t \right)=t\sqrt{1-t}.$
Ta có
$f'\left( t \right)=\sqrt{1-t}+t.\dfrac{-1}{2\sqrt{1-t}}=\dfrac{2-3t}{2\sqrt{1-t}}$
$f'\left( t \right)=0\Leftrightarrow 2-3t=0\Leftrightarrow t=\dfrac{2}{3}$
$\Rightarrow \underset{\left( 0;1 \right)}{\mathop{\max }} f\left( t \right)=f\left( \dfrac{2}{3} \right)=\dfrac{2}{3}.\sqrt{1-\dfrac{2}{3}}=\dfrac{2\sqrt{3}}{9}.$
Vậy thể tích lớn nhất của khối trụ giới hạn bởi hình trụ trên bằng $\dfrac{64}{\pi }.\dfrac{2\sqrt{3}}{9}=\dfrac{128\sqrt{3}}{9\pi }.$
Đáp án D.