Google
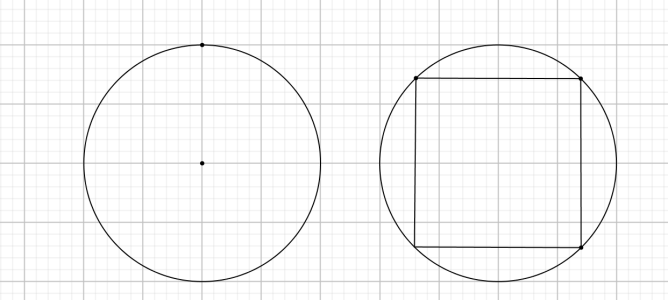
Câu hỏi: Từ một miếng tôn hình tròn bán kính 2 m, người ta cắt ra một hình chữ nhật rồi uốn thành mặt xung quanh của một chiếc thùng phi hình trụ như hình vẽ bên dưới. Để thể tích thùng lớn nhất thì diện tich phần tôn bị cắt bỏ gần nhất với giá trị nào sau đây?
A. $5 m^{2}$.
B. $6 \mathrm{~m}^{2}$.
C. $9 \mathrm{~m}^{2}$.
D. $8 \mathrm{~m}^{2}$.
B. $6 \mathrm{~m}^{2}$.
C. $9 \mathrm{~m}^{2}$.
D. $8 \mathrm{~m}^{2}$.
Gọi cạnh của hình chữ nhật lần lượt là $x,y\ \left( 0<x,y<4 \right)$.
Chiều cao của khối trụ là $y$, bán kính đáy $r=\dfrac{x}{2\pi }$.
Thể tích khối trụ $V=\pi {{\left( \dfrac{x}{2\pi } \right)}^{2}}y=\dfrac{{{x}^{2}}y}{4\pi }$ (1). Theo bài ra ${{x}^{2}}+{{y}^{2}}=16\Rightarrow {{x}^{2}}=16-{{y}^{2}}$ (2).
Thay (2) vào (1) ta được $V=\dfrac{16y-{{y}^{3}}}{4\pi }$ ; $V'=\dfrac{16-3{{y}^{2}}}{4\pi }\Rightarrow {V}'=0\Rightarrow y=\dfrac{4\sqrt{3}}{3}$.
Bảng biến thiên
Thể tích lớn nhất khi $y=\dfrac{4\sqrt{3}}{3}\Rightarrow x=\dfrac{4\sqrt{6}}{3}\Rightarrow {{S}_{ABCD}}=xy=\dfrac{16\sqrt{2}}{3}\left( {{m}^{2}} \right)$.
Diện tích cắt bỏ ${{S}_{1}}=4\pi -{{S}_{ABCD}}=4\pi -\dfrac{16\sqrt{2}}{3}\approx 5.02\left( {{m}^{2}} \right)$.
Chiều cao của khối trụ là $y$, bán kính đáy $r=\dfrac{x}{2\pi }$.
Thể tích khối trụ $V=\pi {{\left( \dfrac{x}{2\pi } \right)}^{2}}y=\dfrac{{{x}^{2}}y}{4\pi }$ (1). Theo bài ra ${{x}^{2}}+{{y}^{2}}=16\Rightarrow {{x}^{2}}=16-{{y}^{2}}$ (2).
Thay (2) vào (1) ta được $V=\dfrac{16y-{{y}^{3}}}{4\pi }$ ; $V'=\dfrac{16-3{{y}^{2}}}{4\pi }\Rightarrow {V}'=0\Rightarrow y=\dfrac{4\sqrt{3}}{3}$.
Bảng biến thiên
Diện tích cắt bỏ ${{S}_{1}}=4\pi -{{S}_{ABCD}}=4\pi -\dfrac{16\sqrt{2}}{3}\approx 5.02\left( {{m}^{2}} \right)$.
Đáp án A.