Google
Câu hỏi: Trung điểm các cạnh của một hình tứ diện đều là đỉnh của
A. Một hình diện đều.
B. Một hình lục giác đều.
C. Một hình chóp tứ giác đều.
D. Một hình bát diện đều.
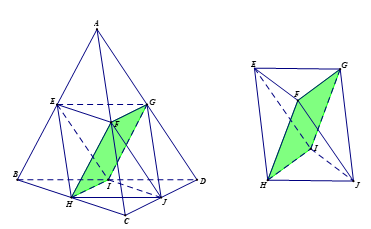
Gọi Tứ diện đều là $ABCD$ cạnh có độ dài $a$.
Gọi $E$, $F$, $G$, $H$, $I$, $J$ lần lượt là trung điểm của các cạnh $AB$, $\text{AC}$,AD, $BC$, $BD$, $CD$. Nối các trung điểm ta được hình bát diện $EFGH\text{IJ}$
Ta có : $EF=EG=EI=EH=JF=JG=JI=JH=FG=FH=IH=IG=\dfrac{a}{2}$
( Vì đều là các đường trung bình của các tam giác đều)
$\Rightarrow $ Các mặt của bát diện là các tam giác đều cạnh có độ dài $\dfrac{1}{2}a$
Mỗi đỉnh của bát diện $EFGH\text{IJ}$ là đỉnh chung của đúng $4$ tam giác đều
$\Rightarrow $ bát diện $EFGH\text{IJ}$ là bát diện đều.
Vậy trung điểm các cạnh của hình tứ diện đều là đỉnh của hình bát diện đều.
A. Một hình diện đều.
B. Một hình lục giác đều.
C. Một hình chóp tứ giác đều.
D. Một hình bát diện đều.
Gọi Tứ diện đều là $ABCD$ cạnh có độ dài $a$.
Gọi $E$, $F$, $G$, $H$, $I$, $J$ lần lượt là trung điểm của các cạnh $AB$, $\text{AC}$,AD, $BC$, $BD$, $CD$. Nối các trung điểm ta được hình bát diện $EFGH\text{IJ}$
Ta có : $EF=EG=EI=EH=JF=JG=JI=JH=FG=FH=IH=IG=\dfrac{a}{2}$
( Vì đều là các đường trung bình của các tam giác đều)
$\Rightarrow $ Các mặt của bát diện là các tam giác đều cạnh có độ dài $\dfrac{1}{2}a$
Mỗi đỉnh của bát diện $EFGH\text{IJ}$ là đỉnh chung của đúng $4$ tam giác đều
$\Rightarrow $ bát diện $EFGH\text{IJ}$ là bát diện đều.
Vậy trung điểm các cạnh của hình tứ diện đều là đỉnh của hình bát diện đều.
Đáp án D.