Google
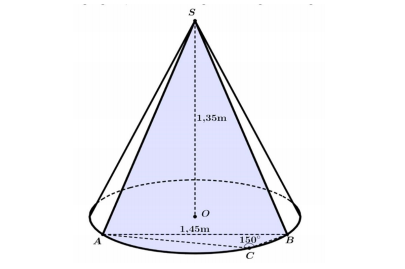
Câu hỏi: Trong khu du lịch sinh thái người ta đặt một mô hình nón lớn với chiều cao $1.35m$ và sơn trang trí hoa văn một phần mặt ngoài của hình nón ứng với cung nhỏ $\overset\frown{AB}$ như hình vẽ. Biết $AB=1.45m,\widehat{ACB}=150{}^\circ $ và giá tiền để sơn trang trí là $3.500.000$ đồng mỗi mét vuông. Hỏi số tiền chi phí (làm tròn đến hàng nghìn) mà người ta cần dùng để trang trí là bao nhiêu?
A. $5.264.000$ đồng.
B. $5.624.000$ đồng.
C. $5.426.000$ đồng.
D. $5.246.000$ đồng.
Gọi $O$, $R$ là bán kính đường tròn ngoại tiếp $\Delta ABC$ cũng là bán kính của đường tròn đáy của hình nón. Khi đó diện tích đường tròn đáy của hình nón là: ${{S}_{(O)}}=\pi {{R}^{2}}$.
Áp dụng định lý sin ta có: $R=\dfrac{AB}{2\sin \widehat{ACB}}=\dfrac{1,45}{2\sin 150{}^\circ }=1,45\Rightarrow R=OA=OB=AB\Rightarrow \Delta ABC$ đều
$\Rightarrow \widehat{AOB}={{60}^{0}}\Rightarrow $ diện tích hình quạt $AOB$ là: ${{S}_{quatAOB}}=\pi .\dfrac{{{R}^{2}}.60{}^\circ }{360{}^\circ }=\dfrac{1}{6}\pi {{R}^{2}}=\dfrac{1}{6}{{S}_{(O)}}$.
Do đó diện tích mặt được sơn chiếm $\dfrac{1}{6}$ diện tích xung quanh của hình nón.
Vì vậy số tiền cần sơn là: $T=\dfrac{1}{6}\pi Rl{{.2.10}^{6}}=\dfrac{1}{6}\pi {{.2.10}^{6}}.1,45.\sqrt{1,{{35}^{2}}+1,{{45}^{2}}}\approx 1,504.3,{{5.10}^{6}}=5.264.000$ đồng.
A. $5.264.000$ đồng.
B. $5.624.000$ đồng.
C. $5.426.000$ đồng.
D. $5.246.000$ đồng.
Áp dụng định lý sin ta có: $R=\dfrac{AB}{2\sin \widehat{ACB}}=\dfrac{1,45}{2\sin 150{}^\circ }=1,45\Rightarrow R=OA=OB=AB\Rightarrow \Delta ABC$ đều
$\Rightarrow \widehat{AOB}={{60}^{0}}\Rightarrow $ diện tích hình quạt $AOB$ là: ${{S}_{quatAOB}}=\pi .\dfrac{{{R}^{2}}.60{}^\circ }{360{}^\circ }=\dfrac{1}{6}\pi {{R}^{2}}=\dfrac{1}{6}{{S}_{(O)}}$.
Do đó diện tích mặt được sơn chiếm $\dfrac{1}{6}$ diện tích xung quanh của hình nón.
Vì vậy số tiền cần sơn là: $T=\dfrac{1}{6}\pi Rl{{.2.10}^{6}}=\dfrac{1}{6}\pi {{.2.10}^{6}}.1,45.\sqrt{1,{{35}^{2}}+1,{{45}^{2}}}\approx 1,504.3,{{5.10}^{6}}=5.264.000$ đồng.
Đáp án A.