Câu hỏi: Trên một sợi dây có sóng dừng tần số góc
A. 160 cm/s.
B.
C.
D. 80 cm/s.
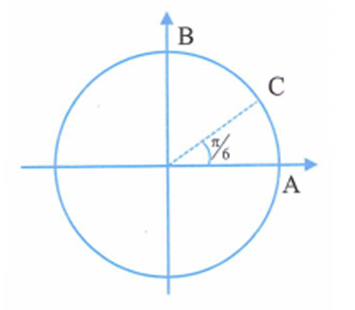
AB là khoảng cách giữa nút và bụng gần nhất:
Mặt khác
Khi sợi dây biến dạng nhiều nhất, khoảng cách giữa A và C là:
Khi B đi đến vị trí có li độ bằng biên độ của
A. 160 cm/s.
B.
C.
D. 80 cm/s.
AB là khoảng cách giữa nút và bụng gần nhất:
Mặt khác
Khi sợi dây biến dạng nhiều nhất, khoảng cách giữa A và C là:
Khi B đi đến vị trí có li độ bằng biên độ của
Đáp án B.