Câu hỏi: Trên mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình ${{u}_{A}}=2cos\left( 30\pi t \right)$ và ${{u}_{B}}=3cos\left( 30\pi t+\pi \right)$, trong đó u tính bằng mm và t tính bằng s. Giả sử tốc độ truyền sóng trên mặt chất lỏng là 60 cm/s và biên độ sóng không đổi trong quá trình truyền sóng. Trên một đường thẳng A nằm trên mặt chất lỏng, đi qua trung điểm của AB, và nghiêng góc 45° so với AB có bao nhiêu điểm dao động với biên độ bằng 1 mm?
A. 6 điểm.
B. 7 điểm.
C. 8 điểm.
D. 9 điểm.
Ta tính được bước sóng là $\lambda =\dfrac{v}{f}=\dfrac{v.2\pi }{\omega }=\dfrac{60.2\pi }{30\pi }=4cm$
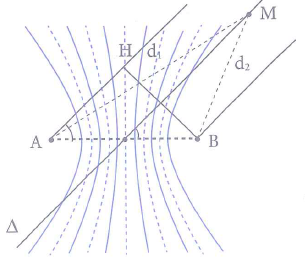
Hạ đoạn BH vuông góc với đường d1 ta có $AH=AB.cos45{}^\circ =10\sqrt{2}cm$
Nhận thấy hai nguồn A, B dao động ngược pha với biên độ sai khác nhau $3-2=1mm$, cho nên những điểm dao động với biên độ 1 mm là những điểm thuộc cực tiểu giao thoa. Điều kiện cực tiểu là ${{d}_{1}}-{{d}_{2}}=n\lambda $.
Xét điểm M nằm trên đường thẳng $\Delta $ thuộc nửa trên của mặt phẳng, khi đó ta có $0\le AM-BM={{d}_{1}}-{{d}_{2}}\le AH$
Kết hợp với điều kiện M thuộc cực tiểu giao thoa ta có: $0\le n\lambda \le 10\sqrt{2}\to 0\le n\le 3,5\to n=0,1,2,3$.
Như vậy nửa trên của đường $\Delta $ có 4 điểm M thỏa mãn điều kiện bài toán ra, trong đó một điểm chính là trung điểm của AB. Do tính đối xứng của hệ vân giao thoa, ở nửa dưới đường A sẽ có thêm 3 điểm M nữa thỏa mãn điều kiện bài toán.
Như vậy tổng số điểm cần tìm là 7 điểm.
A. 6 điểm.
B. 7 điểm.
C. 8 điểm.
D. 9 điểm.
Ta tính được bước sóng là $\lambda =\dfrac{v}{f}=\dfrac{v.2\pi }{\omega }=\dfrac{60.2\pi }{30\pi }=4cm$
Hạ đoạn BH vuông góc với đường d1 ta có $AH=AB.cos45{}^\circ =10\sqrt{2}cm$
Nhận thấy hai nguồn A, B dao động ngược pha với biên độ sai khác nhau $3-2=1mm$, cho nên những điểm dao động với biên độ 1 mm là những điểm thuộc cực tiểu giao thoa. Điều kiện cực tiểu là ${{d}_{1}}-{{d}_{2}}=n\lambda $.
Xét điểm M nằm trên đường thẳng $\Delta $ thuộc nửa trên của mặt phẳng, khi đó ta có $0\le AM-BM={{d}_{1}}-{{d}_{2}}\le AH$
Kết hợp với điều kiện M thuộc cực tiểu giao thoa ta có: $0\le n\lambda \le 10\sqrt{2}\to 0\le n\le 3,5\to n=0,1,2,3$.
Như vậy nửa trên của đường $\Delta $ có 4 điểm M thỏa mãn điều kiện bài toán ra, trong đó một điểm chính là trung điểm của AB. Do tính đối xứng của hệ vân giao thoa, ở nửa dưới đường A sẽ có thêm 3 điểm M nữa thỏa mãn điều kiện bài toán.
Như vậy tổng số điểm cần tìm là 7 điểm.
Đáp án B.