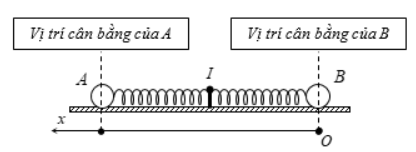
Câu hỏi: Trên mặt phẳng nhắn nằm ngang có hai lò xo cùng độ cứng k và chiều dài tự nhiên 25 cm. Gắn một đầu lò xo vào giá đỡ I cố định, đầu kia gắn với vật nhỏ A, B có khối lượng lần lượt là m và 4m (Hình vẽ). Ban đầu A, B được giữ đứng yên sao cho lò xo gắn A dãn 5 cm, lò xo gắn B nén 5 cm. Đồng thời buông tay để các vật dao động, khi đó khoảng cách nhỏ nhất giữa A và B gần với giá tr

A. 45 cm.
B. 40 cm.
C. 55 cm.
D. 50 cm.
+ Với
Chọn hệ trục tọa độ như hình vẽ, khi đó phương trình li độ của hai dao động được xác định bởi
Nhận thấy tam thức bậc 2 với biến

A. 45 cm.
B. 40 cm.
C. 55 cm.
D. 50 cm.
+ Với
Chọn hệ trục tọa độ như hình vẽ, khi đó phương trình li độ của hai dao động được xác định bởi
Nhận thấy tam thức bậc 2 với biến
Đáp án A.