Google
Câu hỏi: Trên mặt nước tại hai điểm ${{S}_{1}},{{S}_{2}}$ người ta đặt hai nguồn sóng kết hợp dao động điều hòa theo phương thẳng đứng với phương trình ${{u}_{1}}=6\cos \left( 40\pi t \right)$ và ${{u}_{2}}=9\cos \left( 40\pi t \right)$ ( ${{u}_{1}},{{u}_{2}}$ tính bằng mm). Biết tốc độ truyền sóng trên mặt nước là 180cm/s, coi biên độ sóng không đổi khi truyền sóng. Trên đoạn thẳng ${{S}_{1}}{{S}_{2}}$ điểm dao động với biên độ $3\sqrt{19} mm$ và cách trung điểm I của ${{S}_{1}}{{S}_{2}}$ một đoạn gần nhất là:
A. 0,50cm.
B. 0,25cm.
C. 0,75cm.
D. 1,50cm.
A. 0,50cm.
B. 0,25cm.
C. 0,75cm.
D. 1,50cm.
Phương pháp:
Phương trình biên độ của giao thoa sóng
Cách giải:
Bước sóng $\lambda =\dfrac{v}{f}=9 cm.$
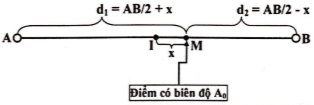
Độ lệch pha hai sóng kết hợp tại M: $\Delta \varphi =\dfrac{2\pi }{\lambda }\left( {{d}_{1}}-{{d}_{2}} \right)=\dfrac{2\pi }{\lambda }.2x$
Biên độ sóng tại M: $A_{M}^{2}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi \Leftrightarrow {{\left( 3\sqrt{19} \right)}^{2}}={{6}^{2}}+{{9}^{2}}+2.6.9\cos \dfrac{4\pi x}{\lambda }$
$\Rightarrow \dfrac{4\pi x}{\lambda }=\dfrac{\pi }{3}\Rightarrow x=\dfrac{\lambda }{12}=0,75 cm.$
Phương trình biên độ của giao thoa sóng
Cách giải:
Bước sóng $\lambda =\dfrac{v}{f}=9 cm.$
Độ lệch pha hai sóng kết hợp tại M: $\Delta \varphi =\dfrac{2\pi }{\lambda }\left( {{d}_{1}}-{{d}_{2}} \right)=\dfrac{2\pi }{\lambda }.2x$
Biên độ sóng tại M: $A_{M}^{2}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi \Leftrightarrow {{\left( 3\sqrt{19} \right)}^{2}}={{6}^{2}}+{{9}^{2}}+2.6.9\cos \dfrac{4\pi x}{\lambda }$
$\Rightarrow \dfrac{4\pi x}{\lambda }=\dfrac{\pi }{3}\Rightarrow x=\dfrac{\lambda }{12}=0,75 cm.$
Đáp án C.