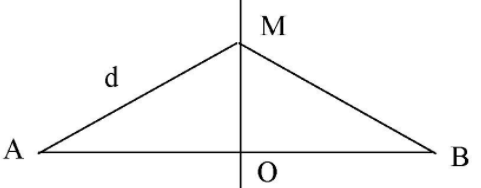
Câu hỏi: Trên mặt nước có hai nguồn sóng $\mathrm{A}, \mathrm{B}$ cách nhau $20 \mathrm{~cm}$ dao động theo phương thẳng đứng với phương trình $\mathrm{u}=1,5 \cos \left(20 \pi \mathrm{t}+\dfrac{\pi}{6}\right) \mathrm{cm}$. Sóng truyền đi với vận tốc $20 \mathrm{~cm} / \mathrm{s}$. Gọi $\mathrm{O}$ là trung điểm $\mathrm{AB}, \mathrm{M}$ là một điểm nằm trên đường trung trực $\mathrm{AB}$ (khác $\mathrm{O}$ ) sao cho $\mathrm{M}$ dao động cùng pha với hai nguồn và gần nguồn nhất; $\mathrm{N}$ là một điểm nằm trên $\mathrm{AB}$ dao động với biên độ cực đại gần $\mathrm{O}$ nhất. Coi biên độ sóng không thay đổi trong quá trình truyền đi. Khoảng cách giữa 2 điểm $\mathrm{M}, \mathrm{N}$ lớn nhất trong quá trình dao động gần nhất với giá trị nào sau đây?
A. 6,8 cm
B. 8,3 cm
C. 10 cm
D. $9,1 \mathrm{~cm}$.
$\lambda =v.\dfrac{2\pi }{\omega }=20.\dfrac{2\pi }{20\pi }=2$ (cm)
$MA=k\lambda =2\lambda >OA=10\Rightarrow k>5\Rightarrow {{k}_{\min }}=6\to MA=12cm$
$MO=\sqrt{M{{A}^{2}}-O{{A}^{2}}}=\sqrt{{{12}^{2}}-{{10}^{2}}}=2\sqrt{11}cm$ và $NO=\dfrac{\lambda }{2}=1cm$
$MN_{\min }^{2}=M{{O}^{2}}+N{{O}^{2}}={{\left( 2\sqrt{11} \right)}^{2}}+{{1}^{2}}=45$
M, N ngược pha và có biên độ ${{A}_{M}}={{A}_{N}}=2a=2.1,5=3$ (cm) và
$\to M{{N}_{\max }}=\sqrt{MN_{\min }^{2}+{{\left( {{A}_{M}}+{{A}_{N}} \right)}^{2}}}=\sqrt{45+{{\left( 3+3 \right)}^{2}}}=9$ (cm).
A. 6,8 cm
B. 8,3 cm
C. 10 cm
D. $9,1 \mathrm{~cm}$.
$\lambda =v.\dfrac{2\pi }{\omega }=20.\dfrac{2\pi }{20\pi }=2$ (cm)
$MA=k\lambda =2\lambda >OA=10\Rightarrow k>5\Rightarrow {{k}_{\min }}=6\to MA=12cm$
$MO=\sqrt{M{{A}^{2}}-O{{A}^{2}}}=\sqrt{{{12}^{2}}-{{10}^{2}}}=2\sqrt{11}cm$ và $NO=\dfrac{\lambda }{2}=1cm$
$MN_{\min }^{2}=M{{O}^{2}}+N{{O}^{2}}={{\left( 2\sqrt{11} \right)}^{2}}+{{1}^{2}}=45$
M, N ngược pha và có biên độ ${{A}_{M}}={{A}_{N}}=2a=2.1,5=3$ (cm) và
$\to M{{N}_{\max }}=\sqrt{MN_{\min }^{2}+{{\left( {{A}_{M}}+{{A}_{N}} \right)}^{2}}}=\sqrt{45+{{\left( 3+3 \right)}^{2}}}=9$ (cm).
Đáp án D.