Câu hỏi: Trên mặt nước có hai nguồn sóng kết hợp A và B cách nhau 68mm, dao động điều hòa cùng pha theo phương vuông góc với mặt nước. Trên đoạn AB, hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 5mm. Điểm C là trung điểm của AB. Trên đường tròn tâm C bán kính 20mm nằm trên mặt nước có bao nhiêu diểm dao động với biên độ cực đại?
A. 20.
B. 16.
C. 18.
D. 14.
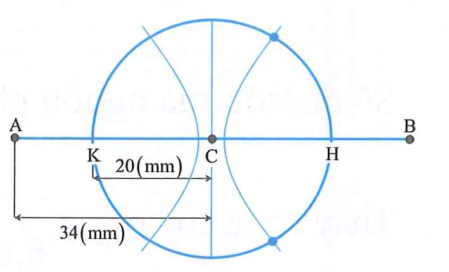
Hai điểm cực đại gần nhau trên đường thẳng nối hai nguồn có vị trí cân bằng cách nhau một khoảng $\dfrac{\lambda }{2}=5\to \lambda =10(mm)$
Các điểm dao động cực đại trên đoạn KH thỏa mãn:
$\dfrac{KA-KB}{\lambda }\le k\le \dfrac{HA-GB}{\lambda }\Leftrightarrow \dfrac{14-54}{10}\le k\le \dfrac{54-24}{10}\Leftrightarrow -4\le k\le 4$
$\Rightarrow k=\left\{ \pm 4;\pm 3;\pm 2;\pm 1;0 \right\}\to $ Có 9 giá trị k thỏa mãn.
Mỗi đường cực đại cắt đường tròn tại 2 điểm (trừ 2 đường cực đại k = 4 và $k=-4$ chỉ cắt đường tròn tại 1 điểm) nên số điểm dao động với biên độ cực đại trên đường tròn là: $7.2+2=16$ điểm.
A. 20.
B. 16.
C. 18.
D. 14.
Hai điểm cực đại gần nhau trên đường thẳng nối hai nguồn có vị trí cân bằng cách nhau một khoảng $\dfrac{\lambda }{2}=5\to \lambda =10(mm)$
Các điểm dao động cực đại trên đoạn KH thỏa mãn:
$\dfrac{KA-KB}{\lambda }\le k\le \dfrac{HA-GB}{\lambda }\Leftrightarrow \dfrac{14-54}{10}\le k\le \dfrac{54-24}{10}\Leftrightarrow -4\le k\le 4$
$\Rightarrow k=\left\{ \pm 4;\pm 3;\pm 2;\pm 1;0 \right\}\to $ Có 9 giá trị k thỏa mãn.
Mỗi đường cực đại cắt đường tròn tại 2 điểm (trừ 2 đường cực đại k = 4 và $k=-4$ chỉ cắt đường tròn tại 1 điểm) nên số điểm dao động với biên độ cực đại trên đường tròn là: $7.2+2=16$ điểm.
Đáp án B.