Câu hỏi: Trên bề mặt chất lỏng có hai nguồn phát sóng kết hợp A, B (AB = 16 cm) dao động cùng biên độ, cùng tần số 25 Hz, cùng pha, coi biên độ sóng không đổi. Biết tốc độ truyền sóng là $80 \mathrm{~cm} / \mathrm{s}$. Điểm P ở mặt chất lỏng nằm trên đường thắng Bz vuông góc với $\mathrm{AB}$ tại $\mathrm{B}$ và cách B một khoảng $12 \mathrm{~cm}$. Điểm dao động với biên độ cực đại nằm trên $\mathrm{Bz}$ cách P một đoạn nhỏ nhất là
A. $0,8 \mathrm{~cm}$.
B. $16,8 \mathrm{~cm}$
C. $3,5 \mathrm{~cm}$
D. $4,8~\text{cm}$.
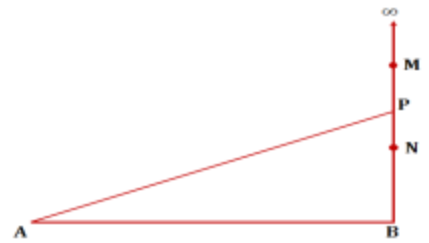
$\lambda =\dfrac{v}{f}=\dfrac{80}{25}=3,2$ (cm)
${{k}_{P}}=\dfrac{PA-PB}{\lambda }=\dfrac{\sqrt{{{16}^{2}}+{{12}^{2}}}-12}{3,2}=2,5$
Trên Bz thì càng xa nguồn khoảng cách giữa cực đại và cực tiểu liên tiếp càng lớn nên ${{k}_{N}}=3$ gần P hơn
${{k}_{N}}=\dfrac{NA-NB}{\lambda }\Rightarrow 3=\dfrac{\sqrt{{{16}^{2}}+N{{B}^{2}}}-NB}{3,2}\Rightarrow NB=\dfrac{128}{15}cm$
$PN=PB-NB=12-\dfrac{128}{15}\approx 3,5cm$.
A. $0,8 \mathrm{~cm}$.
B. $16,8 \mathrm{~cm}$
C. $3,5 \mathrm{~cm}$
D. $4,8~\text{cm}$.
$\lambda =\dfrac{v}{f}=\dfrac{80}{25}=3,2$ (cm)
${{k}_{P}}=\dfrac{PA-PB}{\lambda }=\dfrac{\sqrt{{{16}^{2}}+{{12}^{2}}}-12}{3,2}=2,5$
Trên Bz thì càng xa nguồn khoảng cách giữa cực đại và cực tiểu liên tiếp càng lớn nên ${{k}_{N}}=3$ gần P hơn
${{k}_{N}}=\dfrac{NA-NB}{\lambda }\Rightarrow 3=\dfrac{\sqrt{{{16}^{2}}+N{{B}^{2}}}-NB}{3,2}\Rightarrow NB=\dfrac{128}{15}cm$
$PN=PB-NB=12-\dfrac{128}{15}\approx 3,5cm$.
Đáp án C.