Câu hỏi: Tại O có một nguồn âm (được coi là nguồn điểm) phát sóng âm đẳng hướng với công suất không đổi ra môi trường không hấp thụ âm. Một người cầm máy đo cường độ âm và đi bộ từ A đến C theo một đường thẳng để xác định cường độ âm. Biết rằng, khi đi từ A đến C, cường độ âm tăng từ I đến 4I rồi lại giảm xuống I. Tỉ số
A.
B.
C.
D.
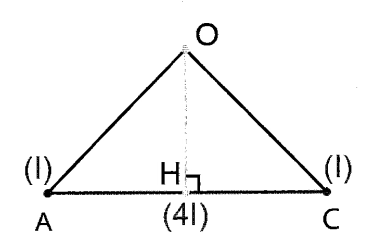
Khi đi từ A đến C theo một đường thẳng, cường độ âm tăng từ I đến 4I rồi lại giảm xuống I, chứng tỏ cường độ âm tại A và C bằng nhau và bằng I (tam giác OAC cân tại O), cường độ âm lớn nhất bằng 4I.
Ta có:
Xét tại điểm A và H ta có mối liên hệ:
Ta có
Vậy tỉ số:
A.
B.
C.
D.
Khi đi từ A đến C theo một đường thẳng, cường độ âm tăng từ I đến 4I rồi lại giảm xuống I, chứng tỏ cường độ âm tại A và C bằng nhau và bằng I (tam giác OAC cân tại O), cường độ âm lớn nhất bằng 4I.
Ta có:
Xét tại điểm A và H ta có mối liên hệ:
Ta có
Vậy tỉ số:
Đáp án C.