Câu hỏi: Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm A cách 0 một đoạn x (m). Trên tia vuông góc với OA tại A lấy điểm B cách A một khoảng 6m. ĐiểmM thuộc đoạn AB sao cho
A. 35
B. 25
C. 15
D. 33
A. 35
B. 25
C. 15
D. 33
Phương pháp:
+ Sử dụng công thức
+ Sử dụng công thức: Hiệu mức cường độ âm:
+ Sử dụng công thức tính cường độ âm:
Cách giải:
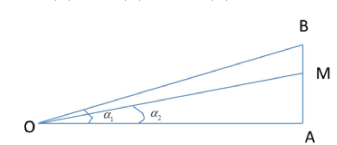
Theo BĐY Cosi, ta có:
Do đó:
Ta có:
Mặt khác:
+ Sử dụng công thức
+ Sử dụng công thức: Hiệu mức cường độ âm:
+ Sử dụng công thức tính cường độ âm:
Cách giải:
Theo BĐY Cosi, ta có:
Do đó:
Ta có:
Mặt khác:
Đáp án D.