Câu hỏi: Tại 2 điểm A và B trên mặt nước cách nhau 16 cm có 2 nguồn kết hợp dao động điều hòa cùng tần số, cùng pha nhau. Điểm M nằm trên mặt nước và nằm trên đường trung trực của AB cách trung điểm I của AB một khoảng nhỏ nhất bằng
A. 9,22 (cm)
B. 2,14 (cm)
C. 8,75 (cm)
D. 8,57 (cm)
Giả sử phương trình sóng tại A, B:
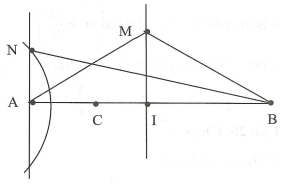
+ Xét điểm M trên trung trực của AB và AM = d
Sóng từ A, B đến M
+ Điểm M dao động cùng pha với I khi
+ Khi k = 0 M trùng với I, M gần I nhất ứng với k = 1 và
Từ đó suy ra:
+ Xét điểm N trên đường vuông góc với AB tại A:
Điểm N dao động với biên độ cực tiểu khi
Khi đó:
Mặt khác:
Lấy (**) – (*) ta được:
A. 9,22 (cm)
B. 2,14 (cm)
C. 8,75 (cm)
D. 8,57 (cm)
Giả sử phương trình sóng tại A, B:
+ Xét điểm M trên trung trực của AB và AM = d
Sóng từ A, B đến M
+ Điểm M dao động cùng pha với I khi
+ Khi k = 0 M trùng với I, M gần I nhất ứng với k = 1 và
Từ đó suy ra:
+ Xét điểm N trên đường vuông góc với AB tại A:
Điểm N dao động với biên độ cực tiểu khi
Khi đó:
Mặt khác:
Lấy (**) – (*) ta được:
Đáp án B.