Câu hỏi: Ở mặt nước, một nguồn sóng đặt tại điểm O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước có bước sóng $\lambda$. Chọn hệ tọa độ vuông góc $\mathrm{Oxy}$ (thuộc mặt nước). Hai điểm $\mathrm{P}$ và $\mathrm{Q}$ nằm trên $\mathrm{Ox}, \mathrm{P}$ dao động ngược pha với $\mathrm{O}$ còn $\mathrm{Q}$ dao động cùng pha với $\mathrm{O}$. Giữa khoảng $\mathrm{OP}$ có 4 điểm dao động ngược pha với $\mathrm{O}$, giữa khoảng $\mathrm{OQ}$ có 8 điểm dao động ngược pha với $\mathrm{O}$. Trên trục Oy có điểm $\mathrm{M}$ sao cho góc $\mathrm{PMQ}$ đạt giá tri lớn nhất. Số điểm dao động ngược pha với $\mathrm{O}$ trên đoạn $\mathrm{MQ}$ là
A. 5.
B. 6.
C. 7.
D. 4.
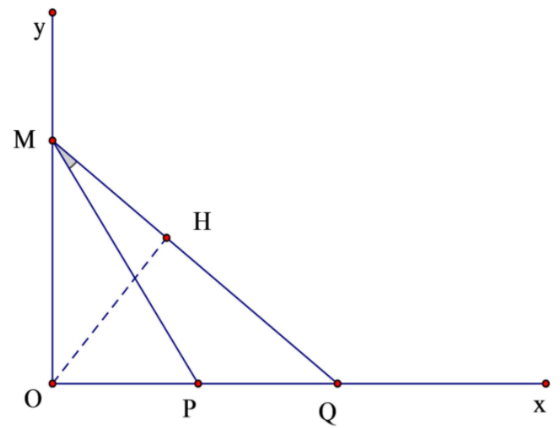
$\tan PMQ=\tan \left( OMQ-OMP \right)=\dfrac{\tan OMQ-\tan OMP}{1+\tan OMQ.\tan OMP}$
$=\dfrac{\dfrac{OQ}{OM}-\dfrac{OP}{OM}}{1+\dfrac{OQ}{OM}.\dfrac{OP}{OM}}=\dfrac{OQ-OP}{OM+\dfrac{OQ.OP}{OM}}\underset{\operatorname{Cos}i}{\mathop{\le }} \dfrac{OQ-OP}{2\sqrt{OQ.OP}}$
Dấu = xảy ra $\Leftrightarrow OM=\dfrac{OQ.OP}{OM}$
$\Rightarrow OM=\sqrt{OQ.OP}=\sqrt{8\lambda .4,5\lambda }=6\lambda $
Kẻ $OH\bot MQ\left( H\in MQ \right)\Rightarrow \dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{Q}^{2}}}=\dfrac{1}{{{\left( 6\lambda \right)}^{2}}}+\dfrac{1}{{{\left( 8\lambda \right)}^{2}}}\Rightarrow OH=4,8\lambda $
Trên MH có $OH\le k\lambda \le OM\Rightarrow 4,8\le k\le 6\Rightarrow $ 1 giá trị k bán nguyên
Trên QH có $OH\le k\lambda \le OQ\Rightarrow 4,8\le k\le 8\Rightarrow $ 3 giá trị k bán nguyên
Vậy trên MQ có $1+3=4$ điểm ngược pha với O.
A. 5.
B. 6.
C. 7.
D. 4.
$\tan PMQ=\tan \left( OMQ-OMP \right)=\dfrac{\tan OMQ-\tan OMP}{1+\tan OMQ.\tan OMP}$
$=\dfrac{\dfrac{OQ}{OM}-\dfrac{OP}{OM}}{1+\dfrac{OQ}{OM}.\dfrac{OP}{OM}}=\dfrac{OQ-OP}{OM+\dfrac{OQ.OP}{OM}}\underset{\operatorname{Cos}i}{\mathop{\le }} \dfrac{OQ-OP}{2\sqrt{OQ.OP}}$
Dấu = xảy ra $\Leftrightarrow OM=\dfrac{OQ.OP}{OM}$
$\Rightarrow OM=\sqrt{OQ.OP}=\sqrt{8\lambda .4,5\lambda }=6\lambda $
Kẻ $OH\bot MQ\left( H\in MQ \right)\Rightarrow \dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{Q}^{2}}}=\dfrac{1}{{{\left( 6\lambda \right)}^{2}}}+\dfrac{1}{{{\left( 8\lambda \right)}^{2}}}\Rightarrow OH=4,8\lambda $
Trên MH có $OH\le k\lambda \le OM\Rightarrow 4,8\le k\le 6\Rightarrow $ 1 giá trị k bán nguyên
Trên QH có $OH\le k\lambda \le OQ\Rightarrow 4,8\le k\le 8\Rightarrow $ 3 giá trị k bán nguyên
Vậy trên MQ có $1+3=4$ điểm ngược pha với O.
Đáp án D.