Câu hỏi: Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng $\lambda $. Trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại. C và D là hai điểm ở mặt nước sao cho ABCD là hình vuông. M là một điểm thuộc cạnh CD và nằm trên vân cực đại giao thoa bậc nhất $\left( MA-MB=\lambda \right)$. Biết phần tử tại M dao động ngược pha với các nguồn. Độ dài AB gần nhất với giá trị nào sau đây?
A. $4,3\lambda .$
B. $4,7\lambda .$
C. $4,6\lambda .$
D. $4,4\lambda .$
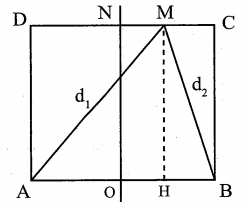
Gọi $AB=L$, vì trên AB có 9 cực đại nên $4\lambda <L<5\lambda $.
$AN=NB=\dfrac{\sqrt{5}}{2}L\to 2\sqrt{5}\lambda <AN<\dfrac{5\sqrt{5}}{2}\lambda $.
Có $\left\{ \begin{aligned}
& MA={{d}_{1}}>AN>4,47\lambda \\
& MB={{d}_{2}}<AN<5,6\lambda \\
& {{d}_{1}}-{{d}_{2}}=\lambda \\
& MA,MB>ON>4\lambda \\
\end{aligned} \right.$
Vì M là cực đại và ngược pha với nguồn nên dao động tại M do A và B truyền đến phải cùng pha nhau và ngược pha với nguồn.
Từ đó ta có bảng giá trị sau:
Ta có: $AB=AH+HB\to \sqrt{d_{1}^{2}-{{L}^{2}}}+\sqrt{d_{2}^{2}-{{L}^{2}}}=1$.
TH1: ${{d}_{1}}=5,5\lambda ;{{d}_{2}}=4,5\lambda \to L\approx 4,377\lambda $.
TH2: ${{d}_{1}}=6,5\lambda ;{{d}_{2}}=5,5\lambda \to L\approx 5,289\lambda $ (loại).
A. $4,3\lambda .$
B. $4,7\lambda .$
C. $4,6\lambda .$
D. $4,4\lambda .$
Gọi $AB=L$, vì trên AB có 9 cực đại nên $4\lambda <L<5\lambda $.
$AN=NB=\dfrac{\sqrt{5}}{2}L\to 2\sqrt{5}\lambda <AN<\dfrac{5\sqrt{5}}{2}\lambda $.
Có $\left\{ \begin{aligned}
& MA={{d}_{1}}>AN>4,47\lambda \\
& MB={{d}_{2}}<AN<5,6\lambda \\
& {{d}_{1}}-{{d}_{2}}=\lambda \\
& MA,MB>ON>4\lambda \\
\end{aligned} \right.$
Vì M là cực đại và ngược pha với nguồn nên dao động tại M do A và B truyền đến phải cùng pha nhau và ngược pha với nguồn.
Từ đó ta có bảng giá trị sau:
| ${{d}_{1}}$ | $5,5\lambda $ | $6,5\lambda $ |
| ${{d}_{2}}$ | $4,5\lambda $ | $5,5\lambda $ |
TH1: ${{d}_{1}}=5,5\lambda ;{{d}_{2}}=4,5\lambda \to L\approx 4,377\lambda $.
TH2: ${{d}_{1}}=6,5\lambda ;{{d}_{2}}=5,5\lambda \to L\approx 5,289\lambda $ (loại).
Đáp án D.