Google
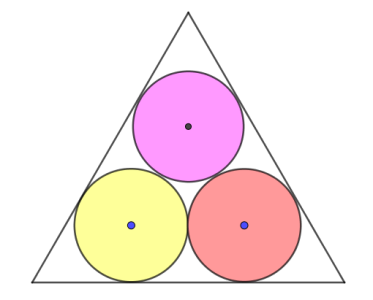
Câu hỏi: Người ta làm một thùng hàng hình lăng trụ tam giác đều có chiều cao $10$ m để chứa ba thiết bị có dạng khối trụ có cùng bán kính đáy là $1$ m và chiều cao $10$ m (với thiết diện mặt cắt như hình vẽ). Thể tích của phần không gian trống trong thùng hàng gần với giá trị nào dưới đây nhất?
A. $35,03 {{\text{m}}^{\text{3}}}$.
B. $30,03 {{\text{m}}^{\text{3}}}$.
C. $5,03 {{\text{m}}^{\text{3}}}$.
D. $15,03 {{\text{m}}^{\text{3}}}$.
Ta có, cạnh đáy của hình lăng trụ bằng
$AB=AM+MN+NB=2AM+{{O}_{1}}{{O}_{2}}=2AM+2$.
Mặt khác, trong tam giác vuông $AM{{O}_{1}}$ có $AM=\dfrac{{{O}_{1}}M}{\tan {{30}^{\circ }}}=\sqrt{3}$ m
Suy ra $AB=2\left( \sqrt{3}+1 \right)\Rightarrow {{S}_{\Delta ABC}}=\dfrac{A{{B}^{2}}\sqrt{3}}{4}=\sqrt{3}{{\left( \sqrt{3}+1 \right)}^{2}}{{\text{m}}^{\text{2}}}$.
Thể tích hình lăng trụ đều bằng ${{V}_{1}}={{S}_{\Delta ABC}}.h=10\sqrt{3}{{\left( \sqrt{3}+1 \right)}^{2}}{{\text{m}}^{\text{3}}}$.
Thể tích một thiết bị có dạng khối trụ bằng ${{V}_{2}}=\pi {{.1}^{2}}.10=10\pi {{\text{m}}^{\text{3}}}$.
Vậy thể tích của phần không gian trống trong thùng hàng bằng
$V={{V}_{1}}-3{{V}_{2}}=10\sqrt{3}{{\left( \sqrt{3}+1 \right)}^{2}}-30\pi \approx 35,03 {{\text{m}}^{\text{3}}}$.
B. $30,03 {{\text{m}}^{\text{3}}}$.
C. $5,03 {{\text{m}}^{\text{3}}}$.
D. $15,03 {{\text{m}}^{\text{3}}}$.
$AB=AM+MN+NB=2AM+{{O}_{1}}{{O}_{2}}=2AM+2$.
Mặt khác, trong tam giác vuông $AM{{O}_{1}}$ có $AM=\dfrac{{{O}_{1}}M}{\tan {{30}^{\circ }}}=\sqrt{3}$ m
Suy ra $AB=2\left( \sqrt{3}+1 \right)\Rightarrow {{S}_{\Delta ABC}}=\dfrac{A{{B}^{2}}\sqrt{3}}{4}=\sqrt{3}{{\left( \sqrt{3}+1 \right)}^{2}}{{\text{m}}^{\text{2}}}$.
Thể tích hình lăng trụ đều bằng ${{V}_{1}}={{S}_{\Delta ABC}}.h=10\sqrt{3}{{\left( \sqrt{3}+1 \right)}^{2}}{{\text{m}}^{\text{3}}}$.
Thể tích một thiết bị có dạng khối trụ bằng ${{V}_{2}}=\pi {{.1}^{2}}.10=10\pi {{\text{m}}^{\text{3}}}$.
Vậy thể tích của phần không gian trống trong thùng hàng bằng
$V={{V}_{1}}-3{{V}_{2}}=10\sqrt{3}{{\left( \sqrt{3}+1 \right)}^{2}}-30\pi \approx 35,03 {{\text{m}}^{\text{3}}}$.
Đáp án A.