Câu hỏi: Một sợi dây OB căng ngang với hai đầu cố định, đang có sóng dừng, sóng truyền trên dây với bước sóng $\lambda $. Hình vẽ bên mô tả hình dạng sợi dây tại 3 thời điểm liên tiếp nhau $t_{l}, t_{2}, t_{3}$. Trong thời điểm $t_{1}$ các phần tử trên dây có cùng tốc độ dao động, biết $t_{2}=t_{1}+\Delta t$ và $t_{3}=t_{2}+2 \Delta t$. Hai điểm M và N trên dây có vị trí cân bằng cách nhau $\dfrac{\lambda}{4}$ mà dao động cùng pha với nhau, có biên độ dao động lần lượt là $A_{M}$ và $A_{N .}$ Giá trị lớn nhất của ${{A}_{M}}+{{A}_{N}}$

A. $10\sqrt{2}~\text{cm}$
B. $5\sqrt{2}~\text{cm}$
C. 10 cm
D. $5\sqrt{3}~\text{cm}$
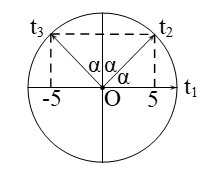
$2\alpha =\dfrac{\pi }{2}\Rightarrow \alpha =\dfrac{\pi }{4}\to 5=A\cos \dfrac{\pi }{4}\Rightarrow A=5\sqrt{2}$ cm
${{A}_{M}}\bot {{A}_{N}}\Rightarrow {{\left( {{A}_{M}}+{{A}_{N}} \right)}_{\max }}=\sqrt{{{A}^{2}}+{{A}^{2}}}=\sqrt{{{\left( 5\sqrt{2} \right)}^{2}}+{{\left( 5\sqrt{2} \right)}^{2}}}=10$ (cm)

A. $10\sqrt{2}~\text{cm}$
B. $5\sqrt{2}~\text{cm}$
C. 10 cm
D. $5\sqrt{3}~\text{cm}$
$2\alpha =\dfrac{\pi }{2}\Rightarrow \alpha =\dfrac{\pi }{4}\to 5=A\cos \dfrac{\pi }{4}\Rightarrow A=5\sqrt{2}$ cm
${{A}_{M}}\bot {{A}_{N}}\Rightarrow {{\left( {{A}_{M}}+{{A}_{N}} \right)}_{\max }}=\sqrt{{{A}^{2}}+{{A}^{2}}}=\sqrt{{{\left( 5\sqrt{2} \right)}^{2}}+{{\left( 5\sqrt{2} \right)}^{2}}}=10$ (cm)
Đáp án C.