Câu hỏi: Một lò xo nhẹ có độ cứng $\mathrm{k}=100 \mathrm{~N} / \mathrm{m}$, đầu trên gắn cố định, đầu dưới treo quả cầu nhỏ $\mathrm{M}$ có khối lượng $500 \mathrm{~g}$ sao cho vật có thể dao động không ma sát theo phương thẳng đứng. Ban đầu vật tựa vào giá đỡ nằm ngang để lò xo bị nén $7,5 \mathrm{~cm}$. Cho giá đỡ chuyển động thẳng đứng xuống dưới với gia tốc $\mathrm{a}=10 \mathrm{~m} / \mathrm{s}^{2}$. Lấy $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$, sau khi $\mathrm{M}$ rời khỏi giá nó dao động điều hòa. Kể từ khi giá đỡ chuyển động cho đến khi lực đàn hồi của lò xo đạt giá trị lớn nhất lần đầu tiên, quãng đường mà vật $\mathrm{M}$ đi được là
A. $15 \mathrm{~cm}$.
B. $17,5 \mathrm{~cm}$.
C. $20 \mathrm{~cm}$.
D. $22,5 \mathrm{~cm}$.
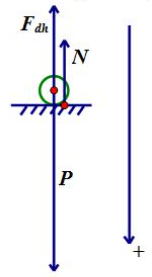
$a=g=10m/{{s}^{2}}\Rightarrow $ vật rời giá đỡ tại vị trí lò xo không biến dạng
$v=\sqrt{2a\Delta {{l}_{n\acute{e}n}}}=\sqrt{2.10.0,075}=0,5\sqrt{6}(m/s)=50\sqrt{6}(cm/s)$
$\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,5}}=10\sqrt{2}$ (rad/s)
$\Delta {{l}_{0}}=\dfrac{mg}{k}=\dfrac{0,5.10}{100}=0,05m=5cm$
$A=\sqrt{\Delta l_{0}^{2}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}=\sqrt{{{5}^{2}}+{{\left( \dfrac{50\sqrt{6}}{10\sqrt{2}} \right)}^{2}}}=10$ (cm)
${{s}_{M}}=\Delta {{l}_{n\acute{e}n}}+\Delta {{l}_{0}}+A=7,5+5+10=22,5$ (cm).
A. $15 \mathrm{~cm}$.
B. $17,5 \mathrm{~cm}$.
C. $20 \mathrm{~cm}$.
D. $22,5 \mathrm{~cm}$.
$a=g=10m/{{s}^{2}}\Rightarrow $ vật rời giá đỡ tại vị trí lò xo không biến dạng
$v=\sqrt{2a\Delta {{l}_{n\acute{e}n}}}=\sqrt{2.10.0,075}=0,5\sqrt{6}(m/s)=50\sqrt{6}(cm/s)$
$\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,5}}=10\sqrt{2}$ (rad/s)
$\Delta {{l}_{0}}=\dfrac{mg}{k}=\dfrac{0,5.10}{100}=0,05m=5cm$
$A=\sqrt{\Delta l_{0}^{2}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}=\sqrt{{{5}^{2}}+{{\left( \dfrac{50\sqrt{6}}{10\sqrt{2}} \right)}^{2}}}=10$ (cm)
${{s}_{M}}=\Delta {{l}_{n\acute{e}n}}+\Delta {{l}_{0}}+A=7,5+5+10=22,5$ (cm).
Đáp án D.