Câu hỏi: Một con lắc lò xo treo thẳng đứng. Từ vị trí cân bằng, nâng vật nhỏ của con lắc theo phương thẳng đứng đến vị trí lò xo không biến dạng rồi buông ra, đồng thời truyền cho vật vận tốc có độ lớn v0 hướng về vị trí cân bằng. Con lắc dao động điều hòa với tần số bằng 5 Hz. Lấy g = 2 = 10m/s2. Trong một chu kì, khoảng thời gian lực kéo về và lực đàn hồi của lò xo tác dụng lên vật ngược hướng nhau bằng
A. 40 cm/s.
B. 30 cm/s.
C. 45 cm/s.
D. 35 cm/s.
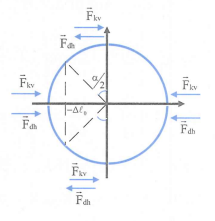
Chọn chiều dương hướng thẳng đứng xuống dưới.
Tại thời điểm t = 0:
Ta có:
Từ đường tròn, kết hợp giả thiết
A. 40 cm/s.
B. 30 cm/s.
C. 45 cm/s.
D. 35 cm/s.
Chọn chiều dương hướng thẳng đứng xuống dưới.
Tại thời điểm t = 0:
Ta có:
Từ đường tròn, kết hợp giả thiết
Đáp án B.