Câu hỏi: Một con lắc lò xo treo thẳng đứng, đầu trên của lò xo được giữ cố định, đầu dưới gắn với một vật nặng. Khi vật nặng đứng cân bằng thì lò xo giãn 4 cm. Cho $g=10m/{{s}^{2}}$ và lấy xấp xỉ ${{\pi }^{2}}=10$. Kích thích cho vật dao động điều hòa theo phương thẳng đứng thì thấy trong môt chu kì dao động, khoảng thời gian lò xo bị nén là $\dfrac{2}{15}s$. Chọn trục tọa độ trùng với phương dao động của vật, chiều dương hướng xuống dưới, gốc tọa độ tại vị trí cân bằng. Chọn gốc thời gian, $t=0$, là lúc vật qua vị trí lò xo giãn 8 cm và đang chuyển động chậm dần. Pha ban đầu của dao động là
A. $\dfrac{\pi }{3}$.
B. $\dfrac{2\pi }{3}$.
C. $-\dfrac{\pi }{3}$.
D. $-\dfrac{2\pi }{3}$.
Khi lò xo cân bằng
${{F}_{dh}}=P\Rightarrow k\Delta \ell =mg\Rightarrow {{\omega }^{2}}=\dfrac{k}{m}=\dfrac{g}{\Delta \ell }$
Chu kì dao động
$T=2\pi \sqrt{\dfrac{\Delta \ell }{g}}=2\pi \sqrt{\dfrac{0,04}{10}}=0,4\left( s \right)$
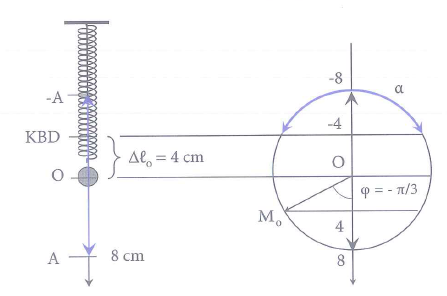
Thời gian lò xo nén trong một chu kì là $\Delta t=\dfrac{2}{15}=\dfrac{T}{3}$ tương ứng với một cung $\alpha =\dfrac{2\pi }{3}$ trên đường tròn (hình vẽ).
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ vị trí không biến dạng đến biên âm rồi trở về vị trí không biến dạng, ta có thể suy luận
$\alpha =\dfrac{2\pi }{3}rad\Rightarrow \Delta \ell =\dfrac{A}{2}\Rightarrow A=2\Delta \ell =8\left( cm \right)$
Khi lò xo giãn 8 cm thì li độ $x=4cm=\dfrac{A}{2}$, do vật đang chuyền động chậm dần nên đang đi ra biên dương, như vậy ban đầu vật đang ở vị trí Mo trên đường tròn $\Rightarrow {{\varphi }_{o}}=-\dfrac{\pi }{3}rad$.
A. $\dfrac{\pi }{3}$.
B. $\dfrac{2\pi }{3}$.
C. $-\dfrac{\pi }{3}$.
D. $-\dfrac{2\pi }{3}$.
Khi lò xo cân bằng
${{F}_{dh}}=P\Rightarrow k\Delta \ell =mg\Rightarrow {{\omega }^{2}}=\dfrac{k}{m}=\dfrac{g}{\Delta \ell }$
Chu kì dao động
$T=2\pi \sqrt{\dfrac{\Delta \ell }{g}}=2\pi \sqrt{\dfrac{0,04}{10}}=0,4\left( s \right)$
Thời gian lò xo nén trong một chu kì là $\Delta t=\dfrac{2}{15}=\dfrac{T}{3}$ tương ứng với một cung $\alpha =\dfrac{2\pi }{3}$ trên đường tròn (hình vẽ).
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ vị trí không biến dạng đến biên âm rồi trở về vị trí không biến dạng, ta có thể suy luận
$\alpha =\dfrac{2\pi }{3}rad\Rightarrow \Delta \ell =\dfrac{A}{2}\Rightarrow A=2\Delta \ell =8\left( cm \right)$
Khi lò xo giãn 8 cm thì li độ $x=4cm=\dfrac{A}{2}$, do vật đang chuyền động chậm dần nên đang đi ra biên dương, như vậy ban đầu vật đang ở vị trí Mo trên đường tròn $\Rightarrow {{\varphi }_{o}}=-\dfrac{\pi }{3}rad$.
Đáp án C.