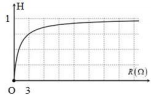
Mắc một biến trở R vào hai cực của một nguồn điện một chiều có...

Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức tính hiệu suất: $H=\dfrac{{{U}_{N}}}{E}=\dfrac{{{R}_{N}}}{{{R}_{N}}+r}$
+ Sử dụng biểu thức tính công suất: $P={{I}^{2}}R$
+ Sử dụng BĐT Cosi
Cách giải:
Ta có: $H=\dfrac{{{U}_{N}}}{E}=\dfrac{{{R}_{N}}}{{{R}_{N}}+r}$
Từ đồ thị ta có tại R = 3Ω thì $H=0,75\Leftrightarrow \dfrac{R}{R+r}=0,75\Leftrightarrow \dfrac{3}{3+r}=0,75\Rightarrow \text{r}=1\Omega $
Công suất tiêu thụ trên $\text{ R: }{{P}_{R}}={{I}^{2}}R=\dfrac{{{E}^{2}}}{{{(R+r)}^{2}}}R=\dfrac{{{E}^{2}}}{{{\left( \sqrt{R}+\dfrac{r}{\sqrt{R}} \right)}^{2}}}\Rightarrow {{P}_{\text{Rmax }}}\text{ khi }{{\left( \sqrt{R}+\dfrac{r}{\sqrt{R}} \right)}^{2}}_{\min }$
Áp dụng BĐT Cosi ta có: $\sqrt{R}+\dfrac{r}{\sqrt{R}}\ge 2\sqrt{r}=2$
$\Rightarrow \sqrt{R}+\dfrac{r}{\sqrt{R}}=2\sqrt{r}=2\text{ khi }\sqrt{R}=\dfrac{r}{\sqrt{R}}\text{ hay }R=r$
$\Rightarrow {{P}_{R\max }}=\dfrac{{{E}^{2}}}{4\text{R}}=\dfrac{{{E}^{2}}}{4\text{r}}=\dfrac{{{6}^{2}}}{4}=9~\text{W}$