Câu hỏi: Lý thuyết Tích vô hướng của hai vecto - SGK Toán 10 Kết nối tri thức
1. GÓC GIỮA HAI VECTO
Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( { \overrightarrow u ,\overrightarrow v } \right)\)
a) Cách xác định góc: Chọn điểm A bất kì, vẽ \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó \(\left( { \overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).
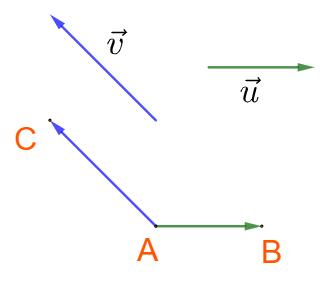
b) Các trường hợp đặc biệt:
+) \(\left( { \overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha \le {180^ \circ }\)
+) \(\left( { \overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v \) hoặc \(\overrightarrow v \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0 \bot \overrightarrow u \forall \overrightarrow u \)
+) \(\left( { \overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng
+) \(\left( { \overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng
2. TÍCH VÔ HƯỚNG CỦA HAI VECTO
+) Tích vô hướng của hai vecto \(\overrightarrow u , \overrightarrow v \): \(\overrightarrow u . \overrightarrow v = \left| {\overrightarrow u } \right|. \left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u , \overrightarrow v } \right)\)
+) \(\overrightarrow u . \overrightarrow v = 0 \Leftrightarrow \overrightarrow u \bot \overrightarrow v \)
+) \(\overrightarrow u . \overrightarrow u = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)
3. BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
a) Biểu thức tọa độ của tích vô hướng
Cho \(\overrightarrow u (x;y)\) và \(\overrightarrow v = (x';y')\).
Khi đó \(\overrightarrow u . \overrightarrow v = xx' + yy'\)
Hệ quả:
+) \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow xx' + yy' = 0\)
+) \({\overrightarrow u ^2} = \overrightarrow u . \overrightarrow u = x.x + y.y = {x^2} + {y^2}\)
+) Tìm góc giữa hai vecto: \(\cos \left( { \overrightarrow u ,\overrightarrow v } \right) = \frac{{ \overrightarrow u .\overrightarrow v }}{{ \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{xx' + yy'}}{{\sqrt {{x^2} + {y^2}} .\sqrt {x{'^2} + y{'^2}} }}\)
b) Công thức tính tích vô hướng khi biết độ dài:
Theo định lí cosin: \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = A{B^2} + A{C^2} - B{C^2}\)
c) Tính chất
Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có:
\(\begin{array}{l}\overrightarrow u . \overrightarrow v = \overrightarrow v . \overrightarrow u \\\overrightarrow u . \left( {\overrightarrow v + \overrightarrow w } \right) = \overrightarrow u . \overrightarrow v + \overrightarrow u . \overrightarrow w \\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u . \overrightarrow v } \right) = \overrightarrow u . \left( {k\overrightarrow v } \right)\end{array}\)
Hệ quả
\(\begin{array}{l}\overrightarrow u . \left( {\overrightarrow v - \overrightarrow w } \right) = \overrightarrow u . \overrightarrow v - \overrightarrow u . \overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2} = {\overrightarrow u ^2} + 2\overrightarrow u . \overrightarrow v + {\overrightarrow v ^2}; {\left( {\overrightarrow u - \overrightarrow v } \right)^2} = {\overrightarrow u ^2} - 2\overrightarrow u . \overrightarrow v + {\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}\)

Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( { \overrightarrow u ,\overrightarrow v } \right)\)
a) Cách xác định góc: Chọn điểm A bất kì, vẽ \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó \(\left( { \overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).
b) Các trường hợp đặc biệt:
+) \(\left( { \overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha \le {180^ \circ }\)
+) \(\left( { \overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v \) hoặc \(\overrightarrow v \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0 \bot \overrightarrow u \forall \overrightarrow u \)
+) \(\left( { \overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng
+) \(\left( { \overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng
2. TÍCH VÔ HƯỚNG CỦA HAI VECTO
+) Tích vô hướng của hai vecto \(\overrightarrow u , \overrightarrow v \): \(\overrightarrow u . \overrightarrow v = \left| {\overrightarrow u } \right|. \left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u , \overrightarrow v } \right)\)
+) \(\overrightarrow u . \overrightarrow v = 0 \Leftrightarrow \overrightarrow u \bot \overrightarrow v \)
+) \(\overrightarrow u . \overrightarrow u = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)
3. BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
a) Biểu thức tọa độ của tích vô hướng
Cho \(\overrightarrow u (x;y)\) và \(\overrightarrow v = (x';y')\).
Khi đó \(\overrightarrow u . \overrightarrow v = xx' + yy'\)
Hệ quả:
+) \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow xx' + yy' = 0\)
+) \({\overrightarrow u ^2} = \overrightarrow u . \overrightarrow u = x.x + y.y = {x^2} + {y^2}\)
+) Tìm góc giữa hai vecto: \(\cos \left( { \overrightarrow u ,\overrightarrow v } \right) = \frac{{ \overrightarrow u .\overrightarrow v }}{{ \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{xx' + yy'}}{{\sqrt {{x^2} + {y^2}} .\sqrt {x{'^2} + y{'^2}} }}\)
b) Công thức tính tích vô hướng khi biết độ dài:
Theo định lí cosin: \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = A{B^2} + A{C^2} - B{C^2}\)
c) Tính chất
Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có:
\(\begin{array}{l}\overrightarrow u . \overrightarrow v = \overrightarrow v . \overrightarrow u \\\overrightarrow u . \left( {\overrightarrow v + \overrightarrow w } \right) = \overrightarrow u . \overrightarrow v + \overrightarrow u . \overrightarrow w \\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u . \overrightarrow v } \right) = \overrightarrow u . \left( {k\overrightarrow v } \right)\end{array}\)
Hệ quả
\(\begin{array}{l}\overrightarrow u . \left( {\overrightarrow v - \overrightarrow w } \right) = \overrightarrow u . \overrightarrow v - \overrightarrow u . \overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2} = {\overrightarrow u ^2} + 2\overrightarrow u . \overrightarrow v + {\overrightarrow v ^2}; {\left( {\overrightarrow u - \overrightarrow v } \right)^2} = {\overrightarrow u ^2} - 2\overrightarrow u . \overrightarrow v + {\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}\)