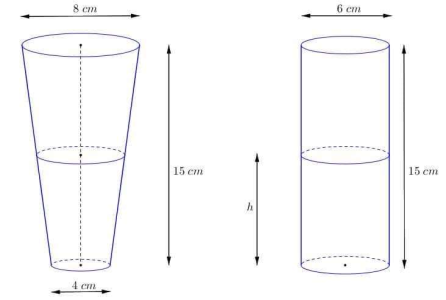
Câu hỏi: Lon nước ngọt có hình trụ còn cốc nước thì có hình nón cụt (như hình vẽ dưới đây). Khi rót nước ngọt từ lon ra cốc thì chiều cao $h$ của phần nước ngọt còn lại trong lon và chiều cao của phần nước ngọt có trong cốc là như nhau. Hỏi khi đó chiều cao $h$ của nước trong lon gần nhất là số nào sau đây?
A. 9,18cm.
B. 14,2cm.
C. 8,58cm.
D. 7,5cm.

A. 9,18cm.
B. 14,2cm.
C. 8,58cm.
D. 7,5cm.
Cách giải:

Thể tích lon nước ngọt lúc đầu là: $V=\pi {{.3}^{2}}.15=135\pi .$
Gọi ${{V}_{1}}$ là thể tích nước ngọt còn lại trong lon sau khi rót ra cốc. Ta có ${{V}_{1}}=\pi {{.3}^{2}}.h=9\pi h.$
Gọi ${{V}_{2}}$ là thể tích nước ngọt đã rót ra.
Ta có: ${{V}_{2}}=\dfrac{\pi h}{3}\left( {{r}^{2}}+r{{'}^{2}}+rr' \right)$ trong đó $r=2,r'$ là bán kính mặt trên của phần nước ngọt trong cốc.
Ta có: $\dfrac{r}{r'}=\dfrac{15}{15+h}\Rightarrow r'=\dfrac{2h+30}{15}$ (do $r=2).$
Vì $V={{V}_{1}}+{{V}_{2}}$ nên ta có: $\dfrac{\pi h}{3}\left[ 4+{{\left( \dfrac{2h+30}{15} \right)}^{2}}+2.\dfrac{2h+30}{15} \right]+9\pi h=135\pi .$
$\Leftrightarrow 4{{h}^{3}}+180{{h}^{2}}+8775h-91125=0\Leftrightarrow h\approx 8,58.$
Thể tích lon nước ngọt lúc đầu là: $V=\pi {{.3}^{2}}.15=135\pi .$
Gọi ${{V}_{1}}$ là thể tích nước ngọt còn lại trong lon sau khi rót ra cốc. Ta có ${{V}_{1}}=\pi {{.3}^{2}}.h=9\pi h.$
Gọi ${{V}_{2}}$ là thể tích nước ngọt đã rót ra.
Ta có: ${{V}_{2}}=\dfrac{\pi h}{3}\left( {{r}^{2}}+r{{'}^{2}}+rr' \right)$ trong đó $r=2,r'$ là bán kính mặt trên của phần nước ngọt trong cốc.
Ta có: $\dfrac{r}{r'}=\dfrac{15}{15+h}\Rightarrow r'=\dfrac{2h+30}{15}$ (do $r=2).$
Vì $V={{V}_{1}}+{{V}_{2}}$ nên ta có: $\dfrac{\pi h}{3}\left[ 4+{{\left( \dfrac{2h+30}{15} \right)}^{2}}+2.\dfrac{2h+30}{15} \right]+9\pi h=135\pi .$
$\Leftrightarrow 4{{h}^{3}}+180{{h}^{2}}+8775h-91125=0\Leftrightarrow h\approx 8,58.$
Đáp án C.