Câu hỏi: Hai vật $m_{1}, m_{2}$ có cùng khối lượng $100 \mathrm{~g}$, được nối với nhau bằng một lò xo nhẹ có độ cứng $k=100 \mathrm{~N} / \mathrm{m}$. Hệ hai vật và lò xo được đặt trên một mặt sàn nằm ngang, trục của lò xo luôn có phương thẳng đứng như hình bên. Ban đầu $m_{2}$ được giữ cố định, đưa $m_{1}$ đến vị trí lò xo bị nén $3,5 \mathrm{~cm}$ rồi truyền cho nó một vận tốc $25\sqrt{3}\pi $ cm/s theo phương thẳng đứng hướng lên trên. Lấy $g=10 \mathrm{~m} / \mathrm{s}^{2}, \pi^{2}=10$. Chọn trục tọa độ thẳng đứng, gốc tọa độ tại vị trí cân bằng của $m_{1}$, chiều dương hướng từ dưới lên. Bỏ qua mọi lực cản. Khi vật $m_{1}$ đi qua vị trí cân bằng lần thứ hai thì thả vật $m_{2}$. Tốc độ trung bình của $m_{1}$ kề từ khi thả $m_{2}$ đến khi $m_{2}$ rời khỏi mặt sàn gần nhất vói giá trị nào sau đây?

A. $1,20 \mathrm{~m} / \mathrm{s}$.
B. $1,06 \mathrm{~m} / \mathrm{s}$.
C. $1,45 \mathrm{~m} / \mathrm{s}$.
D. $1,27 \mathrm{~m} / \mathrm{s}$.
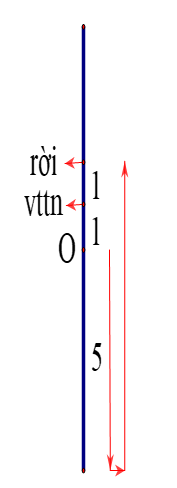
$\Delta {{l}_{0}}=\dfrac{{{m}_{1}}g}{k}=\dfrac{0,1.10}{100}=0,01m=1cm$ và $\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\sqrt{10}\approx 10\pi $ (rad/s)
$A=\sqrt{{{\left( \Delta l-\Delta {{l}_{0}} \right)}^{2}}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}=\sqrt{{{\left( 3,5-1 \right)}^{2}}+{{\left( \dfrac{25\pi \sqrt{3}}{10\pi } \right)}^{2}}}=5$ (cm)
${{m}_{2}}$ rời sàn khi ${{F}_{dhdan}}={{P}_{2}}\Rightarrow k.\Delta {{l}_{dan}}={{m}_{2}}g\Rightarrow \Delta {{l}_{dan}}=\dfrac{{{m}_{2}}g}{k}=\dfrac{0,1.10}{100}=0,01m=1cm$
$x=\Delta {{l}_{dan}}+\Delta {{l}_{0}}=1+1=2$ (cm)
$s=2A+x=2.5+2=12$ (cm)
$t=\dfrac{\pi +\arcsin \dfrac{x}{A}}{\omega }=\dfrac{\pi +\arcsin \dfrac{2}{5}}{10\pi }=0,113$ (s)
${{v}_{tb}}=\dfrac{s}{t}=\dfrac{12}{0,113}\approx 106cm/s=1,06m/s$.

A. $1,20 \mathrm{~m} / \mathrm{s}$.
B. $1,06 \mathrm{~m} / \mathrm{s}$.
C. $1,45 \mathrm{~m} / \mathrm{s}$.
D. $1,27 \mathrm{~m} / \mathrm{s}$.
$\Delta {{l}_{0}}=\dfrac{{{m}_{1}}g}{k}=\dfrac{0,1.10}{100}=0,01m=1cm$ và $\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\sqrt{10}\approx 10\pi $ (rad/s)
$A=\sqrt{{{\left( \Delta l-\Delta {{l}_{0}} \right)}^{2}}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}=\sqrt{{{\left( 3,5-1 \right)}^{2}}+{{\left( \dfrac{25\pi \sqrt{3}}{10\pi } \right)}^{2}}}=5$ (cm)
${{m}_{2}}$ rời sàn khi ${{F}_{dhdan}}={{P}_{2}}\Rightarrow k.\Delta {{l}_{dan}}={{m}_{2}}g\Rightarrow \Delta {{l}_{dan}}=\dfrac{{{m}_{2}}g}{k}=\dfrac{0,1.10}{100}=0,01m=1cm$
$x=\Delta {{l}_{dan}}+\Delta {{l}_{0}}=1+1=2$ (cm)
$s=2A+x=2.5+2=12$ (cm)
$t=\dfrac{\pi +\arcsin \dfrac{x}{A}}{\omega }=\dfrac{\pi +\arcsin \dfrac{2}{5}}{10\pi }=0,113$ (s)
${{v}_{tb}}=\dfrac{s}{t}=\dfrac{12}{0,113}\approx 106cm/s=1,06m/s$.
Đáp án B.