Câu hỏi: Hai vật dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox sao cho không va chạm vào nhau trong quá trình dao động. Vị trí cân bằng của hai vật đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biết phương trình dao động của hai vật lần lượt là x1 = 4cos (4πt + π/3)và x2 =
A. 2017/8 s
B. 2017/4 s
C. 2017/2 s
D. 2017/16 s
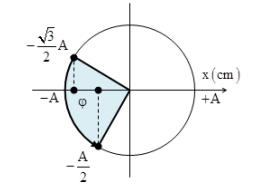
+ Khoảng cách giữa hai vật
+ Trong một chu kì có 4 lần khoảng cách giữa hai vật là 2 cm, vậy ta cần 504 chu kì để được 2016 lần
+ Lần cuối cùng ứng với góc quét
Vậy
A. 2017/8 s
B. 2017/4 s
C. 2017/2 s
D. 2017/16 s
+ Khoảng cách giữa hai vật
+ Trong một chu kì có 4 lần khoảng cách giữa hai vật là 2 cm, vậy ta cần 504 chu kì để được 2016 lần
+ Lần cuối cùng ứng với góc quét
Vậy
Đáp án A.