Câu hỏi: Hai điểm M và N chuyển động tròn đều, cùng chiếu trên một đường tròn tâm O bán kính R với cùng tốc độ dài v = 1 m/s. Biết góc
A. 30,8 cm/s.
B. 86,6 cm/s.
C. 61,5 cm/s.
D. 100 cm/s.
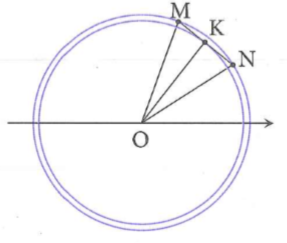
Tốc độ góc của K, M, N bằng nhau và bằng
Dễ thấy
Khi M, N chuyển động tròn đều thì K cũng chuyển động tròn đều với bán kính OK. Do đó, hình chiếu của K xuống một đường kính dao động điều hòa với tần số góc
Vậy
A. 30,8 cm/s.
B. 86,6 cm/s.
C. 61,5 cm/s.
D. 100 cm/s.
Tốc độ góc của K, M, N bằng nhau và bằng
Dễ thấy
Khi M, N chuyển động tròn đều thì K cũng chuyển động tròn đều với bán kính OK. Do đó, hình chiếu của K xuống một đường kính dao động điều hòa với tần số góc
Vậy
Đáp án C.