Câu hỏi: Hai chất điểm M và N dao động điều hòa cùng tần số
A.
B.
C.
D.
A.
B.
C.
D.
Theo đề ta có:
Giả sử chọn j = 0, nghĩa là lúc t = 0:
Tại t1:
Biểu diễn trên hình: Thời điểm t1:
Từ hình vẽ: Dễ thấy 2 thời điểm gần nhất là 2 lần t1:
Từ M1 đến M2:
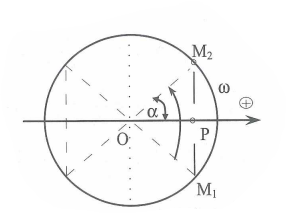
Giả sử chọn j = 0, nghĩa là lúc t = 0:
Tại t1:
Biểu diễn trên hình: Thời điểm t1:
Từ hình vẽ: Dễ thấy 2 thời điểm gần nhất là 2 lần t1:
Từ M1 đến M2:
Đáp án A.