Google
Câu hỏi: Hai chất điểm dao động điều hòa cùng tần số trên hai đường thẳng song song kề nhau cách nhau 5 cm và song song với Ox có đồ thị li độ như hình vẽ. Vị trí cân bằng của hai chất điểm đều ở trên một đường thẳng qua góc tọa độ và vuông góc với Ox. Biết ${{t}_{2}}-t{{}_{1}}$ = 1,08 s. Kể từ lúc t = 0, hai chất điểm cách nhau $5\sqrt{3}$ cm lần thứ 2016 là
A. 362,73 s.
B. 362,85 s.
C. 362,67 s.
D. 362,70 s.
A. 362,73 s.
B. 362,85 s.
C. 362,67 s.
D. 362,70 s.
+ Phương trình dao động của 2 vật: $\left\{ \begin{aligned}
& {{x}_{1}}=5\cos \omega t \\
& {{x}_{2}}=5\sqrt{3}\cos \left( \omega t+\dfrac{\pi }{2} \right) \\
\end{aligned} \right.$
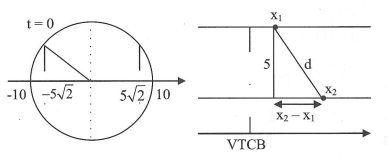+ Khi đồ thị cắt nhau, tức là 2 vật cùng nằm trên một đường thẳng vuông góc với ox, khi đó: ${{x}_{2}}-{{x}_{1}}=0$
$\Rightarrow \omega t=-\dfrac{\pi }{6}+k\pi \Rightarrow \left\{ \begin{aligned}
& {{t}_{1}}=\dfrac{5\pi }{6\omega }\text{ }(k=1) \\
& {{t}_{2}}=\dfrac{23\pi }{6\omega }\text{ }(k=4) \\
\end{aligned} \right.\Rightarrow \omega =\dfrac{3\pi }{1,08}$
+ Gọi d là khoảng cách giữa 2 vật: ${{d}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{5}^{2}}\Rightarrow \left| {{x}_{2}}-{{x}_{1}} \right|=5\sqrt{2}$
+ Bấm máy ${{x}_{2}}-{{x}_{1}}=10\cos \left( \omega t+\dfrac{2\pi }{3} \right)$.
+ Nhận thấy lần thứ 2016 = lần thứ 4 + $\dfrac{2012}{4}$.
+ Thời gian cần tính là: $t=\dfrac{19T}{24}+503T=362,73\text{s}$.
& {{x}_{1}}=5\cos \omega t \\
& {{x}_{2}}=5\sqrt{3}\cos \left( \omega t+\dfrac{\pi }{2} \right) \\
\end{aligned} \right.$
$\Rightarrow \omega t=-\dfrac{\pi }{6}+k\pi \Rightarrow \left\{ \begin{aligned}
& {{t}_{1}}=\dfrac{5\pi }{6\omega }\text{ }(k=1) \\
& {{t}_{2}}=\dfrac{23\pi }{6\omega }\text{ }(k=4) \\
\end{aligned} \right.\Rightarrow \omega =\dfrac{3\pi }{1,08}$
+ Gọi d là khoảng cách giữa 2 vật: ${{d}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{5}^{2}}\Rightarrow \left| {{x}_{2}}-{{x}_{1}} \right|=5\sqrt{2}$
+ Bấm máy ${{x}_{2}}-{{x}_{1}}=10\cos \left( \omega t+\dfrac{2\pi }{3} \right)$.
+ Nhận thấy lần thứ 2016 = lần thứ 4 + $\dfrac{2012}{4}$.
+ Thời gian cần tính là: $t=\dfrac{19T}{24}+503T=362,73\text{s}$.
Đáp án A.
