Gọi $S$ là tập hợp các số phức $z=a+bi \left( a,b\in \mathbb{R}...

Cách 1
Từ giả thiết suy ra $\left| a \right|+\left| b \right|=3\Rightarrow a-b=\pm 3$ (do $ab\le 0$ )
Do $\dfrac{{{z}_{1}}-{{z}_{2}}}{-1+i}$ là số thực dương nên ${{a}_{1}}-{{a}_{2}}=-\left( {{b}_{1}}-{{b}_{2}} \right)<0$ suy ra ${{a}_{1}}<{{a}_{2}}$ và ${{a}_{1}}+{{b}_{1}}={{a}_{2}}+{{b}_{2}}$ (1)
Nếu ${{a}_{1}}-{{b}_{1}}={{a}_{2}}-{{b}_{2}}$ thì ${{z}_{1}}={{z}_{2}}$ (loại);
Vậy ${{a}_{1}}-{{b}_{1}}=-\left( {{a}_{2}}-{{b}_{2}} \right)$ (2)
Từ (1) và (2) suy ra ${{a}_{1}}={{b}_{2}} , {{a}_{2}}={{b}_{1}}\Rightarrow {{a}_{1}}<{{a}_{2}}={{b}_{1}}$
Do đó ${{a}_{1}}-{{b}_{1}}=-3\Rightarrow {{b}_{1}}={{a}_{1}}+3=x+3$
$\Rightarrow {{z}_{1}}=x+\left( x+3 \right)i$, ${{z}_{2}}=x+3+xi$
Vậy $\left| {{z}_{1}}+3i \right|+\left| {{z}_{2}} \right|=\sqrt{{{x}^{2}}+{{\left( x+6 \right)}^{2}}}+\sqrt{{{\left( x+3 \right)}^{2}}+{{x}^{2}}}\ge \sqrt{{{3}^{2}}+{{6}^{2}}}=3\sqrt{5}$
Dấu “=” xảy ra khi $x=-2$.
Cách 2
Từ giả thiết suy ra $\left| a \right|+\left| b \right|=3\Rightarrow a-b=\pm 3$ (do $ab\le 0$ )
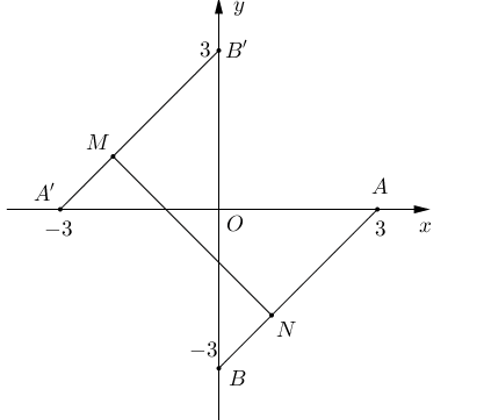
Trên mặt phẳng Oab, vẽ 2 đoạn thẳng
[AB]: $a-b=3 \left( 0\le a\le 3 \right)$ với $A\left( 3;0 \right), B\left( 0;-3 \right)$
[A’B’]: $a-b=-3 \left( -3\le a\le 0 \right)$ với $A'\left( -3;0 \right), B'\left( 0;3 \right)$
Gọi $M\left( a;b \right)$ biểu diễn cho số phức ${{z}_{1}}$, $N\left( a';b' \right)$ biểu diễn cho số phức ${{z}_{2}}$. Thế thì $M,N$ chạy trên [AB] hoặc [A’B’].
Ta có $\dfrac{{{z}_{1}}-{{z}_{2}}}{-1+i}=\dfrac{1}{2}\left[ \left( b-b' \right)-\left( a-a' \right)-\left( a-a' \right)i-\left( b-b' \right)i \right]$
Do $\dfrac{{{z}_{1}}-{{z}_{2}}}{-1+i}$ là số thực dương nên $\left\{ \begin{aligned}
& \left( b-b' \right)-\left( a-a' \right)>0 \\
& \left( b-b' \right)+\left( a-a' \right)=0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a<a' \\
& b>b' \\
& a+b=a'+b' \\
\end{aligned} \right.$
Khi đó $M\in \left[ A'B' \right], N\in \left[ AB \right]$.
Vậy $M\left( a;a+3 \right)$, $N\left( a';a'-3 \right)$
Ta có $a+b=a'+b'\Leftrightarrow a+a-3=a'+a'+3\Leftrightarrow a'=a+3$ nên $N\left( a+3;a \right)$
Do vậy
$\left| {{z}_{1}}+3i \right|+\left| {{z}_{2}} \right|=\sqrt{{{a}^{2}}+{{\left( a+6 \right)}^{2}}}+\sqrt{{{\left( a+3 \right)}^{2}}+{{a}^{2}}}=\sqrt{{{\left( -a \right)}^{2}}+{{\left( a+6 \right)}^{2}}}+\sqrt{{{\left( a+3 \right)}^{2}}+{{\left( -a \right)}^{2}}}$
$\ge \sqrt{{{3}^{2}}+{{6}^{2}}}=3\sqrt{5}$
Dấu “=” xảy ra khi $\dfrac{a+6}{-a}=\dfrac{-a}{a+3}>0\Leftrightarrow a=-2$.