Câu hỏi: Giải mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo
a) Tìm các giá trị còn thiếu trong bảng sau:

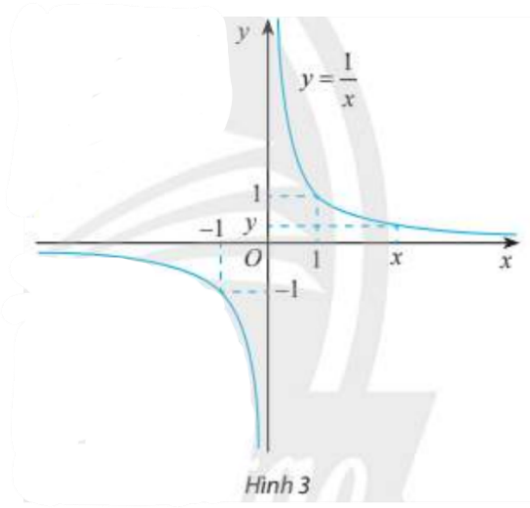
Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Phương pháp giải:
Để điền giá trị vào bảng, ta thay giá trị của \(x\) vào hàm số \(f\left( x \right) = \frac{1}{x}\).
Lời giải chi tiết:
a)
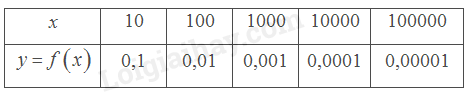
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Phương pháp giải:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {\frac{1}{{{x^2}}} - 3} \right)}}{{{x^2}\left( {1 + \frac{{2x}}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^2}}} - 3}}{{1 + \frac{2}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^2}}} - \mathop {\lim }\limits_{x \to + \infty } 3}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}} = \frac{{0 - 3}}{{1 + 0}} = - 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{1 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to - \infty } 2}}{{\mathop {\lim }\limits_{x \to - \infty } 1 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}} = 0.\frac{2}{{1 + 0}} = 0\).
a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Phương pháp giải:
a) Dựa vào dữ kiện của đề bài, biểu thị mối liên hệ giữa các đại lượng khối lượng muối, lượng nước trong hồ và nồng độ muối để viết biểu thức \(C\left( t \right)\).
b) Vận dụng phương pháp tính giới hạn của hàm số tại vô cực:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) Khối lượng muối có trong hồ là: \(200.10 = 2000\left( {kg} \right)\).
Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(200 + 2t\left( {{m^3}} \right)\).
Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{2000}}{{200 + 2t}}\left( {kg/{m^3}} \right)\)
b) \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{200 + 2t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{t\left( {\frac{{200}}{t} + 2} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{\frac{{200}}{t} + 2}}\)
\( = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\frac{{\mathop {\lim }\limits_{t \to + \infty } 2000}}{{\mathop {\lim }\limits_{t \to + \infty } \frac{{200}}{t} + \mathop {\lim }\limits_{t \to + \infty } 2}} = 0.\frac{{2000}}{{0 + 2}} = 0\)
Ý nghĩa: Khi \(t\) càng lớn thì nồng độ muối càng dần về 0, tức là đến một lúc nào đó nồng độ muối trong hồ không đáng kể, nước trong hồ gần như là nước ngọt.
Hoạt động 4
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.a) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Phương pháp giải:
Để điền giá trị vào bảng, ta thay giá trị của \(x\) vào hàm số \(f\left( x \right) = \frac{1}{x}\).
Lời giải chi tiết:
a)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
Thực hành 4
Tìm các giới hạn sau:a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Phương pháp giải:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {\frac{1}{{{x^2}}} - 3} \right)}}{{{x^2}\left( {1 + \frac{{2x}}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^2}}} - 3}}{{1 + \frac{2}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^2}}} - \mathop {\lim }\limits_{x \to + \infty } 3}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}} = \frac{{0 - 3}}{{1 + 0}} = - 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{1 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to - \infty } 2}}{{\mathop {\lim }\limits_{x \to - \infty } 1 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}} = 0.\frac{2}{{1 + 0}} = 0\).
Vận dụng 1
Một cái hồ đang chứa \(200{m^3}\) nước mặn với nồng độ muối \(10kg/{m^3}\). Người ta ngọt hóa nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ \(2{m^3}/\)phút.a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Phương pháp giải:
a) Dựa vào dữ kiện của đề bài, biểu thị mối liên hệ giữa các đại lượng khối lượng muối, lượng nước trong hồ và nồng độ muối để viết biểu thức \(C\left( t \right)\).
b) Vận dụng phương pháp tính giới hạn của hàm số tại vô cực:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) Khối lượng muối có trong hồ là: \(200.10 = 2000\left( {kg} \right)\).
Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(200 + 2t\left( {{m^3}} \right)\).
Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{2000}}{{200 + 2t}}\left( {kg/{m^3}} \right)\)
b) \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{200 + 2t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{t\left( {\frac{{200}}{t} + 2} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{\frac{{200}}{t} + 2}}\)
\( = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\frac{{\mathop {\lim }\limits_{t \to + \infty } 2000}}{{\mathop {\lim }\limits_{t \to + \infty } \frac{{200}}{t} + \mathop {\lim }\limits_{t \to + \infty } 2}} = 0.\frac{{2000}}{{0 + 2}} = 0\)
Ý nghĩa: Khi \(t\) càng lớn thì nồng độ muối càng dần về 0, tức là đến một lúc nào đó nồng độ muối trong hồ không đáng kể, nước trong hồ gần như là nước ngọt.