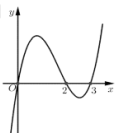
Giả sử $f\left( x \right)$ là một đa thức bậc bốn. Đồ thị hàm số $y=f'\left( 1-x \right)$ được cho như hình bên. Hỏi đồ thị hàm số $g\left( x...

Phương pháp:
- Tính $g'\left( x \right).$
- Giải phương trình $g'\left( x \right)=0$
- Lập BXD $g'\left( x \right).$
Cách giải:
Ta có $g'\left( x \right)=2xf'\left( {{x}^{2}}-3 \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& f'\left( {{x}^{2}}-3 \right)=0 \\
\end{aligned} \right.$
Dựa vào đồ thị hàm số $y=f'\left( 1-x \right)$ ta có $f'\left( 1-x \right)=0\Leftrightarrow \left[ \begin{aligned}
& 1-x=0 \\
& 1-x=2 \\
& 1-x=3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=1 \\
& x=-1 \\
& x=-2 \\
\end{aligned} \right..$
Do đó $f'\left( {{x}^{2}}-3 \right)=0\Leftrightarrow \left[ \begin{aligned}
& {{x}^{2}}-3=1 \\
& {{x}^{2}}-3=-1 \\
& {{x}^{2}}-3=-2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\pm 2 \\
& x=\pm \sqrt{2} \\
& x=\pm 1 \\
\end{aligned} \right..$
Lấy $x=3$ ta có $g'\left( x \right)=6f'\left( 6 \right)<0,$ qua các nghiệm của $g'\left( x \right)=0$ thì $g'\left( x \right)$ đổi dấu.
Bảng xét dấu của $g'\left( x \right):$

Vậy hàm số nghịch biến trên $\left( -1;0 \right).$