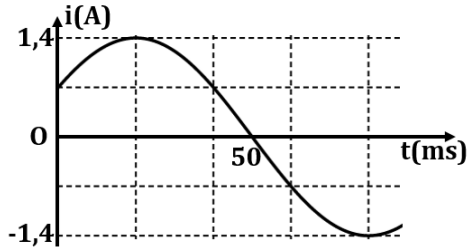
Câu hỏi: Đặt điện áp xoay chiều vào hai bản tụ điện có dung kháng là $Z_{C}=50 \Omega$. Cường độ dòng điện qua tụ điện được mô tả như hình vẽ bên.
Biểu thức điện áp giữa hai bản tụ là
A. $u=70 \sqrt{2} \cos \left(\dfrac{100 \pi t}{3}-\dfrac{\pi}{6}\right) V$.
B. $u=70 \cos \left(\dfrac{50 \pi t}{3}-\dfrac{\pi}{6}\right) V$.
C. $u=70 \sqrt{2} \cos \left(\dfrac{100 \pi t}{3}+\dfrac{\pi}{6}\right) V$.
D. $u=70 \cos \left(\dfrac{50 \pi t}{3}-\dfrac{5 \pi}{6}\right) V$.

Biểu thức điện áp giữa hai bản tụ là
A. $u=70 \sqrt{2} \cos \left(\dfrac{100 \pi t}{3}-\dfrac{\pi}{6}\right) V$.
B. $u=70 \cos \left(\dfrac{50 \pi t}{3}-\dfrac{\pi}{6}\right) V$.
C. $u=70 \sqrt{2} \cos \left(\dfrac{100 \pi t}{3}+\dfrac{\pi}{6}\right) V$.
D. $u=70 \cos \left(\dfrac{50 \pi t}{3}-\dfrac{5 \pi}{6}\right) V$.
${{U}_{0}}={{I}_{0}}{{Z}_{C}}=1,4.50=70$ (V)
Tại $t=0$ thì $i=\dfrac{{{I}_{0}}}{2}\uparrow \Rightarrow {{\varphi }_{i}}=-\dfrac{\pi }{3}\Rightarrow {{\varphi }_{u}}=-\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{5\pi }{6}$
$\omega =\dfrac{\alpha }{t}=\dfrac{\dfrac{\pi }{3}+\dfrac{\pi }{2}}{{{50.10}^{-3}}}=\dfrac{50\pi }{3}$.
Tại $t=0$ thì $i=\dfrac{{{I}_{0}}}{2}\uparrow \Rightarrow {{\varphi }_{i}}=-\dfrac{\pi }{3}\Rightarrow {{\varphi }_{u}}=-\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{5\pi }{6}$
$\omega =\dfrac{\alpha }{t}=\dfrac{\dfrac{\pi }{3}+\dfrac{\pi }{2}}{{{50.10}^{-3}}}=\dfrac{50\pi }{3}$.
Đáp án D.