Câu hỏi: Đặt điện áp xoay chiều u = U0cos(ωt) vào hai đầu đoạn mạch R, L, C mắc nối tiếp, trong đó tụ điện có điện dung C thay đổi. Điều chỉnh C đến giá trị để điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại, khi đó điện áp cực đại hai đầu điện trở là 78 V và tại một thời điểm điện áp hai đầu tụ điện, cuộn cảm và điện trở có độ lớn là 202,8 V; 30 V; uR. Giá trị uR bằng.
A. 30 V.
B. 50 V.
C. 60 V.
D. 40 V.
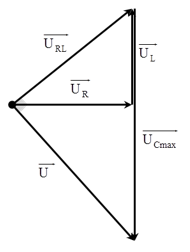
Biểu diễn vecto các điện áp.
Khi
+ Áp dụng hệ thức lượng trong tam giác, ta có:
+ Mặt khác, ta để ý rằng, tại thời điểm t
+ Thay vào phương trình hệ thức lượng ta tìm được
Với hai đại lượng vuông pha
A. 30 V.
B. 50 V.
C. 60 V.
D. 40 V.
Biểu diễn vecto các điện áp.
Khi
+ Áp dụng hệ thức lượng trong tam giác, ta có:
+ Mặt khác, ta để ý rằng, tại thời điểm t
+ Thay vào phương trình hệ thức lượng ta tìm được
Với hai đại lượng vuông pha
Đáp án A.