Câu hỏi: Đặt điện áp xoay chiều
A.
B.
C.
D.
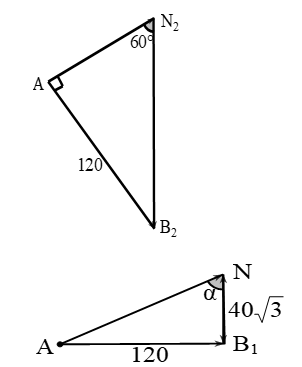
Khi
Khi
A.
B.
C.
D.
Khi
Khi
Đáp án C.